Моделирование на графах
Как найти лучший путь в цифровой вселенной: от навигаторов до теории игр, от алгоритмов Дейкстры до выигрышных стратегий. Это не абстрактная математика — это инструменты, которые работают в твоём смартфоне прямо сейчас.

§ 11. Алгоритмы кратчайших путей — твой GPS в мире графов
Зачем это нужно? Связь с реальным миром
Представь: ты стример, и тебе нужно выбрать оптимальную последовательность игр для марафона, чтобы максимизировать просмотры. Или ты разработчик, который оптимизирует маршрут доставки дронов. Или аналитик, прокладывающий путь данных через серверы так, чтобы минимизировать задержку.
Все эти задачи объединяет одно — поиск оптимального пути. И графы — это универсальный язык для описания таких задач.
🌐 Графы используются везде, где есть:
- Навигация — Google Maps, Яндекс.Карты
- Социальные сети — кратчайший путь между пользователями
- Игровой ИИ — поиск пути персонажа
- Сетевая маршрутизация — как пакеты данных путешествуют по интернету
- Логистика — оптимизация цепочек поставок
- Анализ данных — поиск зависимостей в больших данных
11.1. Три способа найти кратчайший путь
Когда мы говорим о «кратчайшем пути», мы имеем в виду:
Минимальное число рёбер между вершинами
Минимальная сумма весов рёбер
Есть три основных подхода к решению этой задачи. Давай разберём каждый.
Метод 1: Дерево решений (для ориентированных графов)
❓ Когда использовать?
Когда нужно подсчитать количество всех возможных путей из точки A в точку B.
💡 Суть
Представь себе дерево, где каждая ветка — это возможный выбор. Мы просто перебираем все варианты и считаем, сколько путей ведёт к цели.
🎮 Пример из жизни
Ты планируешь цепочку стримов на неделю. Каждый день ты можешь выбрать одну из нескольких игр. Сколько различных последовательностей игр ты можешь создать за неделю?
Это типичная задача на дерево решений. Каждый узел дерева — это день, каждая ветка — выбор игры, листья дерева — возможные комбинации.
⚠️ Важный момент
Этот метод хорош для подсчёта вариантов, но не всегда даёт самый быстрый способ найти оптимальный путь.
Метод 2: Алгоритм Дейкстры (для взвешенных графов)

Алгоритм Дейкстры работает как умный исследователь: всегда выбирает ближайшую непосещённую точку
❓ Когда использовать?
Когда нужно найти кратчайший путь от одной вершины до всех остальных.
🎯 Суть алгоритма
Представь, что ты исследуешь карту в RPG, где каждая локация соединена с другими дорогами разной длины. Ты начинаешь в стартовой точке и постепенно «открываешь» ближайшие локации, всё время запоминая кратчайший известный путь до каждой из них.
Как это работает:
Инициализация
Присваиваем стартовой вершине метку «0» (расстояние до самой себя = 0). Всем остальным — «бесконечность» (∞), потому что мы пока не знаем, как до них добраться.
Итерация
Выбираем непосещённую вершину с минимальной меткой. Смотрим на всех её соседей. Для каждого соседа проверяем: можем ли мы добраться до него быстрее через текущую вершину? Если да — обновляем метку соседа. Помечаем текущую вершину как «посещённую».
Завершение
Когда все вершины посещены, метки показывают кратчайшие расстояния от старта до каждой вершины.
💚 Ключевая идея
Мы всегда двигаемся от «ближайших» вершин к «дальним», при этом гарантируя, что найденное расстояние — действительно кратчайшее.
Разбор примера:
Давай посмотрим на граф из учебника:
Начальное состояние:
A(0) → B(∞), D(∞), C(∞)
↓
Веса: A→B = 5, A→D = 10, A→C = 15
Шаг 1: Выбираем вершину A (метка = 0)
- Обновляем соседей:
• B: 0 + 5 = 5
• D: 0 + 10 = 10
• C: 0 + 15 = 15
- Помечаем A как посещённую
Шаг 2: Выбираем B (минимальная метка = 5)
- Смотрим на соседей B (например, D и E)
- D: сравниваем 10 (текущая метка) и 5 + 9 = 14 → не обновляем
- E: 5 + 14 = 19 → новая метка
- Помечаем B как посещённую
Шаг 3: Выбираем D (метка = 10)
- Обновляем соседей:
• C: сравниваем 15 и 10 + 3 = 13 → обновляем до 13
• E: сравниваем 19 и 10 + 10 = 20 → не обновляем
• F: 10 + 8 = 18 → новая метка
И так далее, пока все вершины не будут посещены.🎮 Пример из программирования
Алгоритм Дейкстры используется в игровых движках для поиска пути врагов к игроку. Вес ребра может означать не только расстояние, но и «опасность» маршрута или затраты энергии.
⚠️ Важное ограничение
Алгоритм Дейкстры не работает с отрицательными весами рёбер! Для таких случаев используют алгоритм Беллмана-Форда.
Метод 3: Динамическое программирование (для задач с ограничениями)

Динамическое программирование решает задачу шаг за шагом: каждое решение опирается на лучшие результаты предыдущих шагов
❓ Когда использовать?
Когда нужно найти оптимальный путь с дополнительными условиями (например, можно двигаться только вправо и вверх, или нужно минимизировать штрафы).
💡 Суть
Разбиваем задачу на этапы и на каждом этапе принимаем оптимальное решение, опираясь на результаты предыдущих этапов.
Пример: Лабиринт с штрафами
Персонаж игры проходит лабиринт. В каждой клетке есть штрафные баллы. Можно двигаться только вверх или вправо. Как пройти лабиринт с минимальными штрафами?
📋 Решение:
- Создаём таблицу, где каждая ячейка соответствует клетке лабиринта
- Заполняем таблицу снизу вверх и слева направо
- Для каждой ячейки выбираем минимум из двух путей (снизу или слева) и прибавляем штраф текущей ячейки
Пример из учебника:
Исходный лабиринт: Заполненная таблица:
3 3 6 11 3 5 13 22
5 3 8 8 9 10 17
3 2 8 8
A 9 1 8 A 9 10 17
Заполнение:
- Начинаем с A: записываем значение (например, 0 + штраф A)
- Для следующей ячейки справа: берём предыдущее значение + штраф текущей
- Для ячейки сверху: аналогично
- Для ячеек, куда можно попасть двумя путями: выбираем минимумПрименение в реальности:
- Оптимизация ресурсов в играх
- Планирование производства
- Финансовые модели
- Алгоритмы сжатия данных
- Выравнивание последовательностей ДНК
- Машинное обучение
🎯 Ключевые выводы
🤔 Проверь себя
Кейсы для применения знаний на практике
Кейс 1: Оптимизация стрима
Ты планируешь марафон на Twitch из 5 игр. Переход от одной игры к другой занимает разное время на подготовку (настройка, загрузка, объяснение зрителям). Как найти последовательность игр с минимальным временем переходов?
Подумай: Какой алгоритм поможет? Как представить задачу в виде графа?
Кейс 2: Маршрутизация в сети
Пакет данных нужно отправить от сервера A к серверу Z. Между серверами есть разные маршруты с разной скоростью передачи. Некоторые каналы могут быть перегружены (большие веса). Как найти самый быстрый маршрут?
Подумай: Какой алгоритм использовать? Почему?
Кейс 3: Игровая задача
В RPG твой персонаж может двигаться только по диагонали вправо-вверх или вправо. На карте есть бонусы (положительные) и ловушки (отрицательные очки). Как пройти с максимальным количеством очков?
Вопросы:
- Можно ли использовать алгоритм Дейкстры? Почему да/нет?
- Какой метод подойдёт лучше?
- Как изменится решение, если разрешить движение в любом направлении?
Челлендж: Объясни младшему
Попробуй объяснить алгоритм Дейкстры человеку, который знает только основы математики. Придумай свою аналогию (не используя примеры из этого материала).
§ 11.2. Теория игр: математика стратегических решений
Выигрышная стратегия — это план игры, где каждый ход продуман заранее
От богатырей до искусственного интеллекта
Помнишь задачу про Алёшу Поповича и девятиглавого змея? Это не просто детская загадка — это введение в теорию игр, раздел математики, который используется в:
- Разработке игрового ИИ
- Экономике и бизнесе
- Политике
- Биологии (эволюция)
- Кибербезопасности
- Машинном обучении
🎲 Что такое игра в математическом смысле?
Это не обязательно шахматы или крестики-нолики. Это любая ситуация, где:
- Есть несколько участников (игроков)
- У каждого есть варианты действий
- Результат зависит от выбора всех участников
- Интересы участников могут не совпадать
Основные понятия
Текущее состояние игры (например, количество голов змея, количество камней на столе)
Переход из одной позиции в другую
Позиция, из которой игрок может гарантированно выиграть при правильной игре
Позиция, из которой игрок обречён на поражение при оптимальной игре противника
Набор правил, следуя которым игрок выигрывает независимо от действий противника
Разбор примера: Алёша и девятиглавый змей
📜 Условия:
- Начальное состояние: 9 голов
- Ход: срубить 1, 2 или 3 головы
- Победа: срубить последнюю голову (довести до 0)
- Игроки: Алёша (первый) и Добрыня (второй)
Анализ методом обратного хода:
Начнём с конца — с победных позиций.
9 8 7 6 5 4 3 2 1 0
В В В ПОБЕДАПозиции 3, 2, 1 — выигрышные, потому что из них можно одним ходом дойти до 0.
Теперь позиция 4. Из неё любой ход (−1, −2, −3) переводит противника в выигрышную позицию (3, 2 или 1). Значит, позиция 4 — проигрышная:
9 8 7 6 5 4 3 2 1 0
П В В ВДвигаемся дальше. Позиции 7, 6, 5 позволяют одним ходом перевести противника в позицию 4. Значит, они выигрышные:
9 8 7 6 5 4 3 2 1 0
В В В П В В ВПозиция 8 — проигрышная (любой ход переводит в выигрышную для противника).
Позиция 9 — выигрышная (можно перейти в позицию 8).
✅ Вывод
Алёша выигрывает, если первым ходом срубит 1 голову (переведя Добрыню в позицию 8).
🎯 Выигрышная стратегия Алёши:
- Первый ход: срубить 1 голову (9 → 8)
- После любого хода Добрыни перевести его в позицию 4 (проигрышную)
- Далее на каждый ход Добрыни отвечать так, чтобы поддерживать проигрышные позиции для него
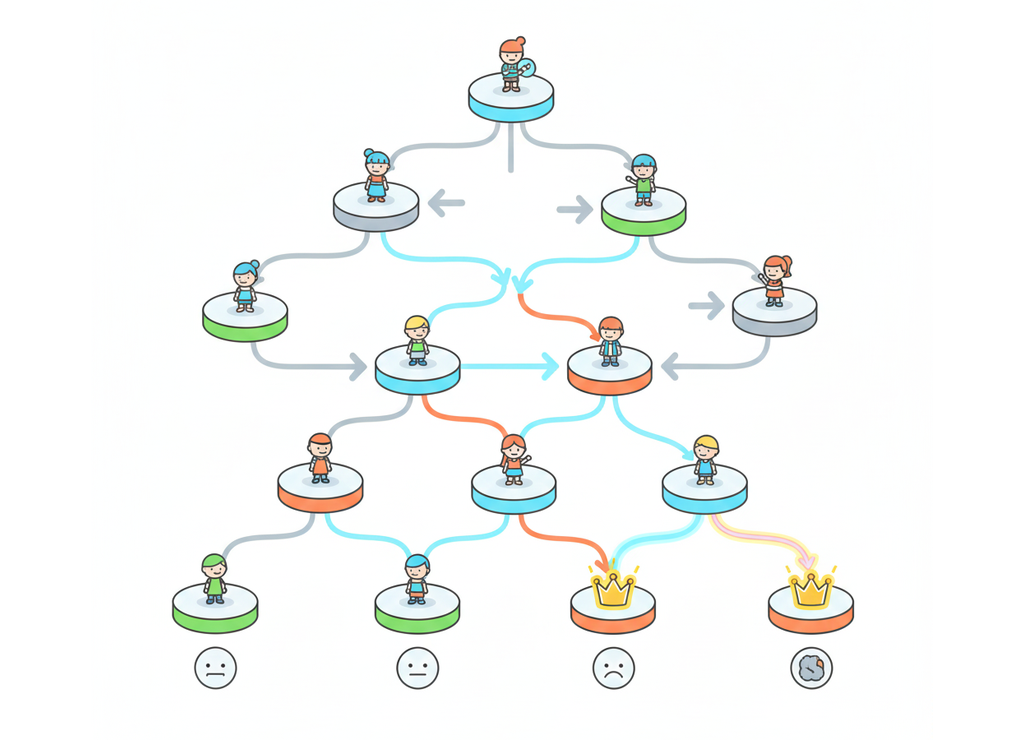
Дерево показывает все возможные варианты игры и выигрышный путь
Заметь: Алёша всегда переводит Добрыню в позицию 4, откуда тот неизбежно переведёт Алёшу в выигрышную позицию (3, 2 или 1).
Пример посложнее: Игра с камнями (задача из ЕГЭ)
📜 Условия:
- Начальное состояние: S камней в куче (1 ≤ S ≤ 45)
- Ходы: +1, +2 или ×3
- Цель: довести до 46+ камней
- Игроки: Петя (первый), Ваня (второй)
Анализ:
Шаг 1: Выигрыш первым ходом
Петя может выиграть сразу, если S ≥ 16:
S ×3 ≥ 48 (для S ≥ 16)Позиции 16–45 — выигрышные для Пети.
Шаг 2: Проигрышные позиции для Пети
Позиция S = 15:
15 + 1 = 16 (В для Вани)
15 + 2 = 17 (В для Вани)
15 × 3 = 45 (В для Вани)Любой ход Пети переводит Ваню в выигрышную позицию. Значит, S = 15 — проигрышная для Пети.
Шаг 3: Выигрыш Пети вторым ходом
Если Петя может перевести Ваню в позицию 15, то после хода Вани Петя окажется в выигрышной позиции.
Как получить 15?
- 14 + 1 = 15 ✓
- 13 + 2 = 15 ✓
- 5 × 3 = 15 ✓
Позиции 5, 13, 14 — выигрышные для Пети (выигрыш вторым ходом).
Шаг 4: Проигрышная позиция для Пети
S = 12:
12 + 1 = 13 (В для Вани вторым ходом)
12 + 2 = 14 (В для Вани вторым ходом)
12 × 3 = 36 (В для Вани первым ходом)Любой ход Пети приводит к выигрышу Вани. Значит, S = 12 — проигрышная для Пети.
💡 Важный паттерн
Заметь закономерность:
- Позиции, из которых можно попасть только в выигрышные — проигрышные
- Позиции, из которых можно попасть хотя бы в одну проигрышную — выигрышные
Это принцип минимакса: игрок выбирает ход, минимизирующий максимально возможный проигрыш.
Игры с полной информацией
Все рассмотренные примеры — игры с полной информацией: участники знают все предыдущие ходы и возможные стратегии.
📌 Примеры:
- Шахматы
- Го
- Крестики-нолики
- Шашки
⚡ Важно
В играх с полной информацией всегда существует оптимальная стратегия!
Для некоторых игр (крестики-нолики) она полностью вычислена. Для других (шахматы, го) — вычислительно сложна, поэтому используют приближённые алгоритмы (минимакс, альфа-бета отсечение, метод Монте-Карло).
Применение в программировании и AI
- Алгоритм минимакс (шахматные движки)
- Альфа-бета отсечение (оптимизация минимакса)
- Метод Монте-Карло (AlphaGo)
- Анализ конкурентных рынков
- Теория аукционов
- Ценообразование
- Моделирование атак и защиты
- Анализ стратегий злоумышленников
- Оптимизация защитных механизмов
🎯 Ключевые выводы по теории игр
🤔 Проверь себя: Теория игр
Кейс 1: Модификация игры со змеем
Условия те же (9 голов, можно срубить 1-3), но теперь проигрывает тот, кто срубил последнюю голову. У кого выигрышная стратегия? Опиши её.
Кейс 2: Игра "21"
Два игрока по очереди добавляют к счётчику число от 1 до 3. Начальное значение — 0. Проигрывает тот, кто получит 21 или больше. У кого выигрышная стратегия при первом ходе?
Подсказка: Проанализируй методом обратного хода. Какие позиции проигрышные?
Кейс 3: Nim-игра (классика теории игр)
Есть несколько куч камней. За ход можно взять любое количество камней из одной кучи. Проигрывает тот, кто не может сделать ход (камни закончились).
Начальная позиция: две кучи по 3 и 5 камней.
Вопросы:
- Есть ли у первого игрока выигрышная стратегия?
- Как изменится ответ для куч (3, 3)?
- Для куч (4, 5)?
Подумай: Можешь ли найти общую закономерность?
Челлендж: Создай свою игру
Придумай свою игру с:
- Чётким начальным состоянием
- Правилами ходов
- Условием победы/поражения
Проанализируй её: есть ли выигрышная стратегия у первого игрока?
📚 Для любознательных
Если тебя заинтересовала теория игр, рекомендуем:
📖 Книга
Александр Шень "Игры и стратегии с точки зрения математики" (доступна бесплатно)
🎥 Видео
3Blue1Brown — визуализации игр и стратегий
♟️ Практика
lichess.org — играй в шахматы с анализом ходов (увидишь алгоритмы в действии)
🎓 Курс
Khan Academy — Game Theory (на английском, но с субтитрами)