Структурное программирование на языке C
Структурное программирование — это не просто набор правил. Это философия создания программ, которая превращает хаос кода в организованную архитектуру. Готов разобраться, как писать программы, которые будут понятны не только компьютеру, но и людям?

Введение: Когда код становится архитектурой
Представь, что тебе нужно построить небоскрёб. Можно ли просто начать складывать кирпичи один на другой, надеясь, что всё как-нибудь само сложится? Конечно, нет. Нужен чертёж, фундамент, каркас, система коммуникаций. То же самое и с программами: когда они разрастаются до тысяч строк кода, без продуманной архитектуры превращаются в хаос.
💡 Определение
Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).
Исторический контекст: Революция Дейкстры
В начале 1960-х программирование было похоже на дикий запад. Программисты использовали команду goto, что превращало код в «спагетти»: следить за логикой было почти невозможно.
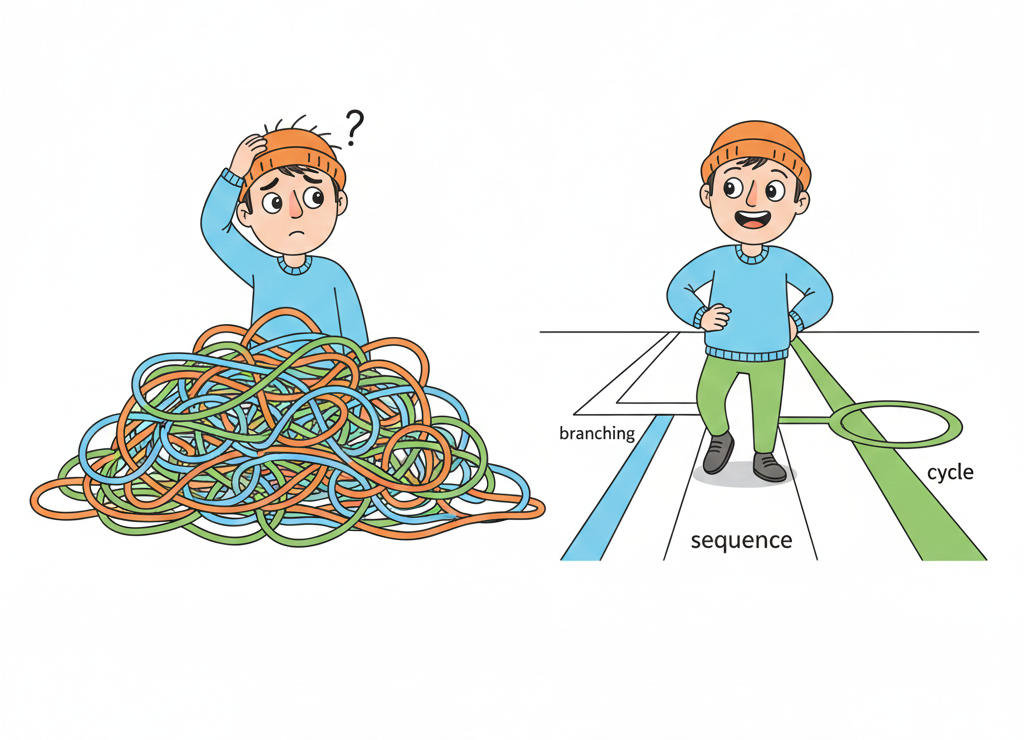
От «кодовых спагетти» к структурированным алгоритмам: революция читаемости
📜 Прорыв 1968 года
Нидерландский учёный Эдсгер Дейкстра опубликовал знаменитую статью «Go To Statement Considered Harmful».
Его идея: любую программу можно построить из трёх базовых конструкций — последовательность, ветвление, цикл — без использования goto.
🎯 Почему это важно для тебя?
- Современные языки (Python, JavaScript, C) построены на этих принципах
- Без структурного подхода невозможно работать в команде
- Язык C стал одним из первых массовых языков, реализовавших идеи структурного программирования
Пять принципов структурного программирования
Эти принципы — фундамент современной разработки ПО. Понимание их делает тебя не просто кодером, а инженером.
Три базовые конструкции
Любую задачу можно решить, комбинируя:
- Последовательность — шаги один за другим
- Ветвление — выбор пути:
if (...) {...} else {...} - Цикл — повторение:
while (...),for (...)
Почему три? Это минимальный набор, достаточный для выражения любой вычислимой функции (доказано математически!).
Вложенность конструкций
Можно вкладывать циклы в условия, условия в циклы произвольным образом.
Аналогия: Как в матрёшке — одна кукла внутри другой, но каждая сама по себе целостный объект.
Функции
Если фрагмент кода повторяется или логически целостен, выноси его в отдельную функцию.
Пример из жизни: Ты не описываешь каждый раз, как открыть дверь, а говоришь: «Открой дверь». Это — функция.
Один вход, один выход
Каждый блок (функция, цикл, условие) должен иметь чётко определённое начало и конец.
Это упрощает отладку: ты точно знаешь, где что начинается и заканчивается.
Метод «сверху вниз»
Сначала пиши общую структуру программы, используя «заглушки» (пустые функции). Затем постепенно заполняй детали.
Аналогия: Сначала пишешь план эссе, потом раскрываешь каждый пункт.
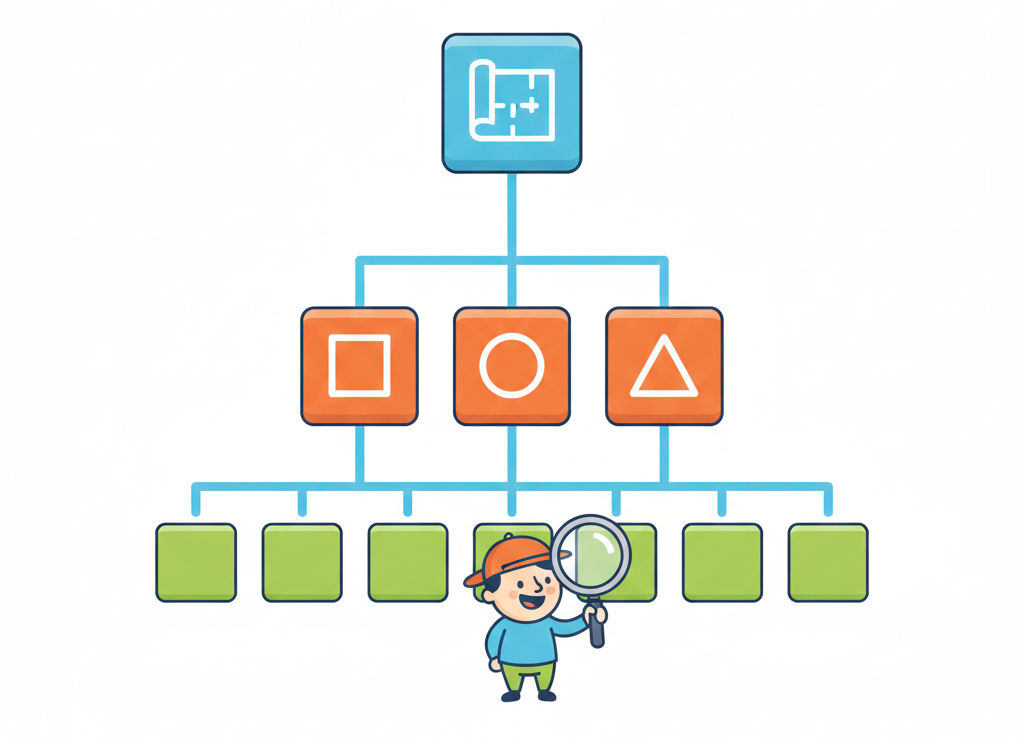
Метод «сверху вниз»: от общего замысла к деталям, сохраняя видимость целого
Функции в C: Кирпичики сложности
Функция — это логически целостный фрагмент кода, который решает подзадачу. Вместо копирования формулы три раза, создаём функцию.
✨ Преимущества функций
- Переиспользование: Написал один раз — используешь многократно
- Читаемость: Вместо формулы — понятное имя функции
- Отладка: Ошибка ищется в одном месте
📋 Синтаксис функции
тип_результата имя_функции(параметры) {
// тело функции
return результат;
}💡 Пример: Вычисление длины отрезка
Формула из геометрии для вычисления длины отрезка по координатам концов:
#include <math.h>
double dlina_otrezka(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
Функции — модульные блоки, которые легко комбинировать благодаря чётким интерфейсам
Прототипы функций и порядок объявления
В C принято объявлять функции до их использования. Если функция определена после main(), нужен прототип.
🔍 Структура программы с прототипом
#include <stdio.h>
#include <math.h>
// Прототип функции (объявление)
double dlina_otrezka(double x1, double y1, double x2, double y2);
int main() {
double d = dlina_otrezka(0, 0, 3, 4);
printf("Длина: %.2f\n", d); // Выведет: 5.00
return 0;
}
// Определение функции (реализация)
double dlina_otrezka(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}Параметры: передача по значению и по указателю
В C параметры по умолчанию передаются по значению (копируются). Если нужно изменить исходную переменную, используй указатели.
📋 Передача по значению
Изменяется только локальная копия:
void increment(int x) {
x = x + 1; // изменяется копия
}
int main() {
int a = 5;
increment(a);
printf("%d\n", a); // Выведет: 5
return 0;
}📍 Передача по указателю
Изменяется оригинальная переменная:
void increment(int *x) {
*x = *x + 1; // изменяется оригинал
}
int main() {
int a = 5;
increment(&a); // передаём адрес
printf("%d\n", a); // Выведет: 6
return 0;
}💡 Аналогия
Передача по значению — это как дать другу ксерокопию документа. Он может делать с ней что угодно, оригинал не изменится.
Передача по указателю — дать адрес сейфа с оригиналом. Теперь друг может изменить сам документ.
Рекурсия: Когда функция вызывает саму себя
Рекурсия — это метод решения задач, при котором функция вызывает саму себя с изменёнными параметрами.
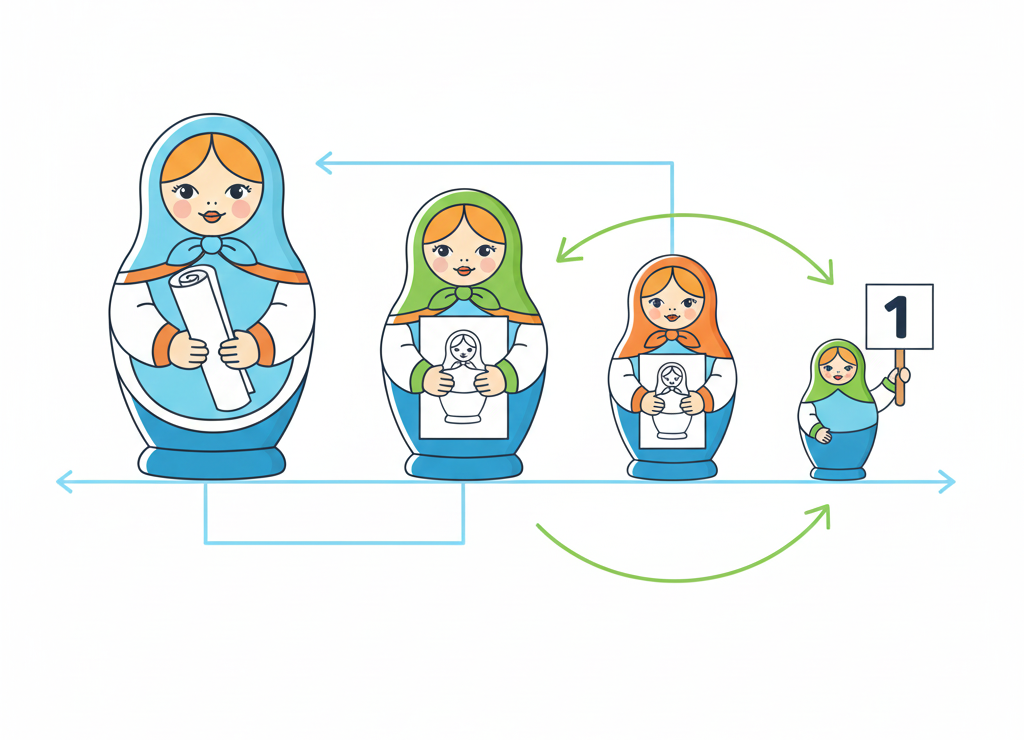
Рекурсия: каждый шаг упрощает задачу до базового случая, затем результаты собираются обратно
📌 Классический пример: Факториал
Математическое определение: n! = 1 × 2 × 3 × ... × n
Рекурсивное определение:
- F(n) = 1, если n ≤ 1
- F(n) = n × F(n-1), если n > 1
Код на C:
#include <stdio.h>
int factorial(int n) {
if (n <= 1) {
return 1; // базовый случай
} else {
return n * factorial(n - 1); // рекурсивный вызов
}
}
int main() {
printf("5! = %d\n", factorial(5)); // Выведет: 120
return 0;
}⚠️ Критически важно: Граничное условие
Без условия остановки рекурсия будет вызывать себя бесконечно (переполнение стека!).
Граничное условие — это момент, когда функция перестаёт обращаться к себе и возвращает результат напрямую.
Практический пример: Сумма цифр числа
Вычислим сумму цифр натурального числа с помощью рекурсии.
💭 Рекурсивная логика
- Если n < 10, то сумма цифр равна самому числу (базовый случай)
- Иначе: сумма цифр n = последняя цифра (n % 10) + сумма цифр оставшейся части (n / 10)
Код:
#include <stdio.h>
int summa_cifr(int n) {
if (n < 10) {
return n; // базовый случай
} else {
return (n % 10) + summa_cifr(n / 10); // рекурсия
}
}
int main() {
printf("Сумма цифр 12345: %d\n", summa_cifr(12345));
// Выведет: 15
return 0;
}🔄 Рекурсия
- Элегантна для задач с естественной вложенностью
- Идеальна для деревьев, обхода графов
- Использует стек вызовов
➿ Итерация
- Эффективнее по памяти
- Не создаёт множество вызовов в стеке
- Подходит для простых циклических задач
📊 Факториал итеративно (для сравнения)
int factorial_iter(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}Практика: Периметр треугольника на C
Применим метод «сверху вниз» для решения реальной задачи.
📝 Задача
Дано три точки A, B, C с координатами. Найти периметр треугольника ABC.
🔷 Шаг 1: Общая структура с заглушкой
#include <stdio.h>
#include <math.h>
// Прототип функции
double dlina_otrezka(double x1, double y1, double x2, double y2);
int main() {
double xa, ya, xb, yb, xc, yc, p;
// Ввод координат
printf("Введите координаты точки A (xa ya): ");
scanf("%lf %lf", &xa, &ya);
printf("Введите координаты точки B (xb yb): ");
scanf("%lf %lf", &xb, &yb);
printf("Введите координаты точки C (xc yc): ");
scanf("%lf %lf", &xc, &yc);
// Вычисление периметра
p = dlina_otrezka(xa, ya, xb, yb) +
dlina_otrezka(xb, yb, xc, yc) +
dlina_otrezka(xc, yc, xa, ya);
printf("Периметр треугольника: %.2f\n", p);
return 0;
}
// Заглушка (пока возвращает 0)
double dlina_otrezka(double x1, double y1, double x2, double y2) {
return 0;
}Преимущество подхода: Сначала проверили логику программы (правильно ли вызываются функции?), затем заполнили детали.
🔷 Шаг 2: Реализация функции
double dlina_otrezka(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}Обобщение: n-угольник
Как модифицировать программу для n-угольника? Храним координаты в массивах и используем цикл.
🔺 Программа для n-угольника
#include <stdio.h>
#include <math.h>
double dlina_otrezka(double x1, double y1, double x2, double y2);
int main() {
int n;
printf("Введите количество вершин: ");
scanf("%d", &n);
double x[n], y[n];
// Ввод координат
for (int i = 0; i < n; i++) {
printf("Координаты вершины %d (x y): ", i + 1);
scanf("%lf %lf", &x[i], &y[i]);
}
// Вычисление периметра
double p = 0;
for (int i = 0; i < n; i++) {
int next = (i + 1) % n; // следующая вершина
p += dlina_otrezka(x[i], y[i], x[next], y[next]);
}
printf("Периметр %d-угольника: %.2f\n", n, p);
return 0;
}
double dlina_otrezka(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}Почему (i + 1) % n? Чтобы замкнуть контур: после последней вершины (i = n-1) идёт первая (индекс 0).
Продвинутая рекурсия: Динамическое программирование
Рассмотрим задачу подсчёта количества программ для исполнителя Плюс.
🎯 Постановка задачи
Исполнитель Плюс имеет три команды:
- +1 (прибавить 1)
- +2 (прибавить 2)
- +4 (прибавить 4)
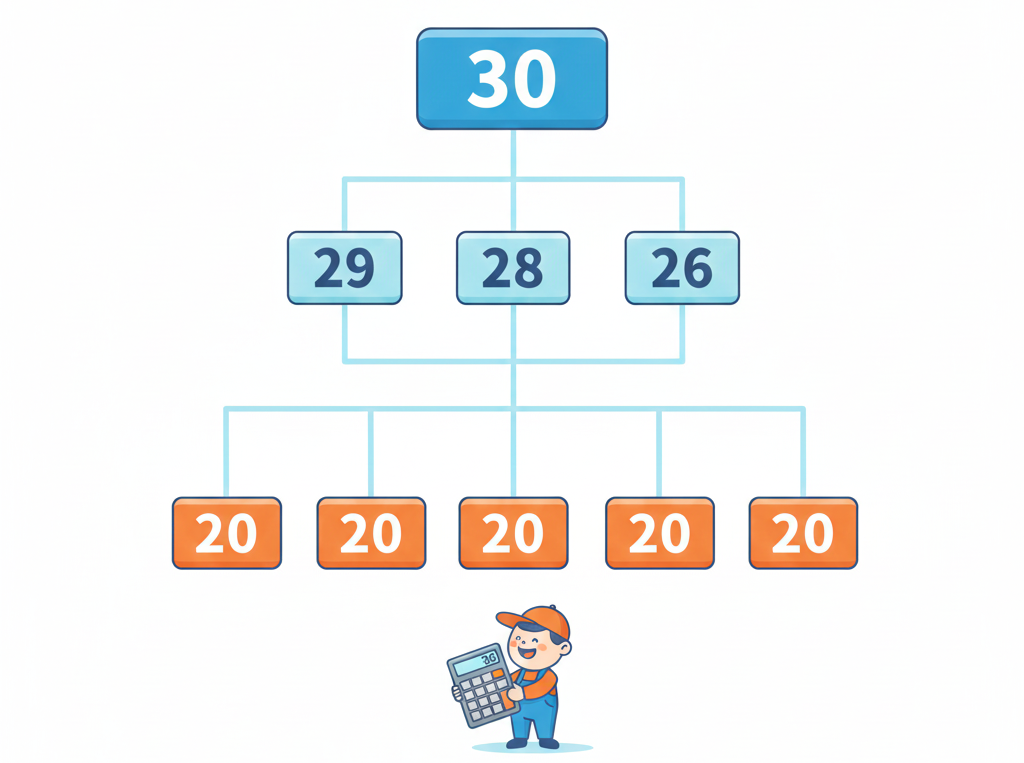
Вопрос: Сколько существует программ, превращающих число 20 в число 30?
Рекурсивное дерево вычислений: каждый путь от листа к корню — возможная программа
🧮 Рекурсивное решение
Обозначим количество программ для получения числа n как K(n).
Базовый случай:
- K(n) = 0 при n < 20 (невозможно получить)
- K(20) = 1 (пустая программа)
Рекурсивный шаг:
Число n можно получить из n-1, n-2 или n-4:
K(n) = K(n-1) + K(n-2) + K(n-4) при n > 20
❌ Наивная рекурсия (неэффективная)
#include <stdio.h>
int K(int n) {
if (n < 20) {
return 0;
} else if (n == 20) {
return 1;
} else {
return K(n-1) + K(n-2) + K(n-4);
}
}
int main() {
printf("K(30) = %d\n", K(30));
return 0;
}Проблема: Функция многократно пересчитывает одни и те же значения!
✅ Итеративный подход (оптимизация)
#include <stdio.h>
int main() {
int K[31];
// Базовые случаи
for (int i = 0; i < 20; i++) {
K[i] = 0;
}
K[20] = 1;
// Заполнение таблицы
for (int i = 21; i <= 30; i++) {
K[i] = K[i-1] + K[i-2] + K[i-4];
}
printf("Ответ: K(30) = %d\n", K[30]);
return 0;
}Преимущество: Каждое значение вычисляется ровно один раз. Сложность O(n)!
📊 Результаты вычислений
| n | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| K(n) | 1 | 1 | 2 | 3 | 6 | 10 | 18 | 31 | 55 | 96 | 169 |
Ответ: 169 различных программ
Рекурсия в природе и культуре
Рекурсивные структуры окружают нас повсюду!
Фракталы — геометрическое воплощение рекурсии: каждая часть повторяет структуру целого
🌿 Природные примеры
- Фракталы в растениях: Лист папоротника — каждая ветвь повторяет форму всего листа
- ДНК: Процесс репликации — молекула копирует саму себя
- Снежинки: Кристаллическая структура с повторяющимися паттернами
🎨 Культурные примеры
- «Дом, который построил Джек»: Каждая строфа включает предыдущую + новый элемент
- Эффект Дросте: Изображение, содержащее само себя (упаковка какао)
- Мемы: Мем про мем про мем...
🔺 Треугольник Серпинского
Алгоритм построения:
- Возьми равносторонний треугольник
- Раздели его на 4 маленьких (средними линиями)
- Удали центральный
- Повтори шаги 2-3 для каждого оставшегося треугольника
Базовый случай: Когда размер треугольника < 1 пиксель — прекрати.
Работа с массивами и указателями
В C массивы передаются по указателю (даже если синтаксически выглядит как передача массива).
📊 Пример: Функция нахождения максимума в массиве
#include <stdio.h>
int find_max(int arr[], int size) {
int max = arr[0];
for (int i = 1; i < size; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
int main() {
int numbers[] = {3, 7, 2, 9, 1};
int size = sizeof(numbers) / sizeof(numbers[0]);
printf("Максимум: %d\n", find_max(numbers, size));
// Выведет: 9
return 0;
}Важно: Размер массива нужно передавать отдельным параметром, так как функция не знает его размер!
🔄 Пример: Функция обмена значений
#include <stdio.h>
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
int main() {
int x = 5, y = 10;
printf("До обмена: x = %d, y = %d\n", x, y);
swap(&x, &y);
printf("После обмена: x = %d, y = %d\n", x, y);
// Выведет: x = 10, y = 5
return 0;
}🔁 Рекурсивный поиск максимума
#include <stdio.h>
int max_recursive(int arr[], int n) {
// Базовый случай: один элемент
if (n == 1) {
return arr[0];
}
// Рекурсивный случай
int max_rest = max_recursive(arr, n - 1);
return (arr[n - 1] > max_rest) ? arr[n - 1] : max_rest;
}
int main() {
int numbers[] = {3, 7, 2, 9, 1, 5};
int size = sizeof(numbers) / sizeof(numbers[0]);
printf("Максимум: %d\n", max_recursive(numbers, size));
return 0;
}Логика: Максимум массива из n элементов — это больший из последнего элемента и максимума первых (n-1) элементов.
🎯 Ключевые выводы
Подведём итоги: что важно запомнить о структурном программировании.
🤔 Проверь себя
Вопросы для самопроверки и закрепления материала
1. В чём заключается сущность структурного программирования? Какие преимущества обеспечивает эта технология?
Подумай о читаемости кода, модульности, возможности работы в команде...
2. Какие три базовые конструкции используются в структурном программировании?
Вспомни: последовательность, ветвление, цикл. Почему именно эти три?
3. Чем отличается передача параметров по значению от передачи по указателю?
Что происходит с оригинальной переменной в каждом случае?
4. Что такое рекурсия? Приведи примеры рекурсивных структур из природы или культуры.
Вспомни фракталы, матрёшки, эффект Дросте...
5. Почему в рекурсивных функциях обязательно должно быть граничное условие?
Что случится без базового случая?
6. Опиши метод разработки программы «сверху вниз». В чём его преимущества?
Как работают заглушки? Зачем сначала создавать общую структуру?
7. Зачем в C нужны прототипы функций?
Что происходит, если функция вызывается до её определения?
8. В каких случаях рекурсивное решение лучше итерационного, а в каких — хуже?
Критерии для сравнения:
- Скорость выполнения
- Потребление памяти
- Читаемость кода
- Естественность алгоритма
📝 Практические задания
Применение знаний на практике — лучший способ обучения!
✍️ Задание 1: Рекурсивная функция
Дана функция:
int F(int n) {
if (n <= 0) return 2;
return F(n-2) + F(n-1) + F(n/2);
}Вопрос: Чему равно F(10)?
Подсказка: Построй таблицу значений от F(0) до F(10).
🎯 Задание 2: Исполнитель Калькулятор
Команды:
- +1 (прибавить 1)
- ×2 (умножить на 2)
Вопросы:
- Сколько программ превращают 1 в 20?
- Сколько из них проходят через число 15?
🔢 Задание 3: Модификация программы
Напиши программу на C, которая:
- Вычисляет площадь треугольника по координатам вершин (формула Герона)
- Обобщает решение для n-угольника
🔍 Задание 4: Анализ рекурсии
Дана программа:
void F(int n) {
if (n > 0) {
F(n - 4);
printf("%d ", n);
F(n / 3);
}
}
int main() {
F(9);
return 0;
}Вопрос: Что выведет программа? Нарисуй дерево вызовов.
💻 Задание 5: Числа Фибоначчи
Напиши на C:
- Рекурсивную функцию для вычисления чисел Фибоначчи
- Итеративную версию той же функции
- Сравни время выполнения для n = 40
🧮 Задание 6: Комбинаторика
Напиши программу вычисления биномиальных коэффициентов:
Cnk = n! / ((n-k)! × k!)
Используй функцию для вычисления факториала.
🚀 Следующие шаги
Куда двигаться дальше для углубления знаний?
📚 Изучить глубже
- Указатели и динамическое выделение памяти (
malloc,free) - Структуры данных (стек, очередь, связные списки)
- Работа с файлами в C
- Многомерные массивы и их применение
🎨 Попробовать на практике
- Создать рекурсивный алгоритм рисования фракталов
- Реализовать алгоритмы сортировки (быструю, пирамидальную)
- Написать программу для работы с текстовыми файлами
- Изучить алгоритмы на графах (поиск в глубину/ширину)
💡 Философия структурного мышления
Когда ты пишешь код, задавай себе вопросы:
- Можно разбить на подзадачи? → Используй функции
- Есть повторяющаяся структура? → Применяй циклы или рекурсию
- Логика понятна через месяц? → Если нет, рефактори
Эти навыки универсальны: они применимы к дизайну приложений, управлению проектами, даже к планированию жизни. Структурное мышление — это инструмент, который превращает хаос в порядок.