Логические операции и логические выражения
Привет! Представь, что твой мозг — это суперкомпьютер, который постоянно принимает решения: идти гулять или доделать домашку, смотреть новое видео или уже лечь спать. Каждое такое решение — это логическая операция! Сегодня мы научимся думать как компьютер.

§ 2.2.1. Логические переменные и логические значения
В алгебре логики мы не работаем с числами типа 5, 10 или 3.14. Нам нужны только два варианта: правда или ложь.
💡 Что такое логическая переменная?
Это высказывание, которое может быть либо истинным (правда), либо ложным (неправда). Без вариантов «может быть» или «наверное».
🔢 Логические значения
В математике мы обозначаем эти значения:
- 1 (единица) = ИСТИНА = правда = true = да
- 0 (ноль) = ЛОЖЬ = неправда = false = нет
Эти 0 и 1 называются логическими значениями.

Логические значения — это всегда выбор из двух: 1 или 0
📱 Примеры из жизни
- «На улице идёт дождь» — логическая переменная (либо идёт, либо нет)
- «Мне нравится эта игра» — тоже логическая переменная
- «Завтра будет контрольная» — ага, снова истина или ложь
🖥️ Зачем это нужно?
Вся цифровая техника работает именно на этом принципе! Когда ты скачиваешь файл, смотришь стрим, играешь в игру — процессор твоего устройства обрабатывает миллиарды операций с нулями и единицами. Алгебра логики — это язык, на котором компьютеры «думают».
§ 2.2.2. Логические операции
Теперь самое интересное — как эти нули и единицы можно комбинировать! Для этого существуют логические операции. Это как математические действия (+, -, ×), только для логики.
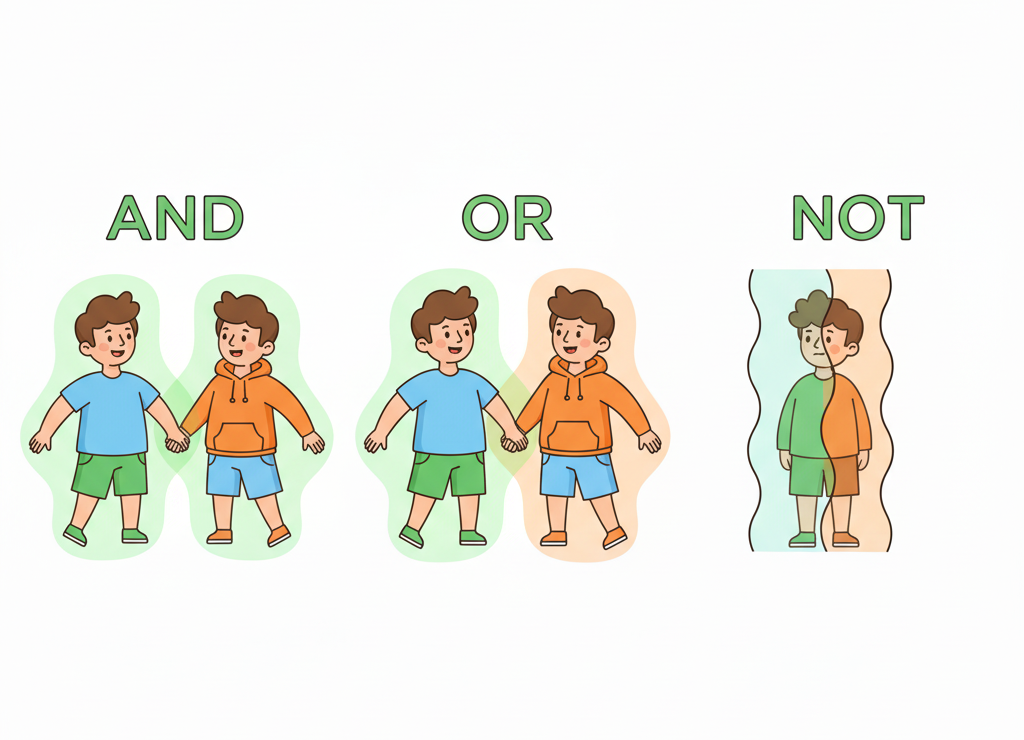
Три кита логики: И, ИЛИ, НЕ
Три главные операции:
🤝 И (конъюнкция) — символ ∧ или &
Результат будет истинным (1) ТОЛЬКО если ОБА условия истинны.
| A | B | A И B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Пример из жизни:
«Я пойду гулять, ЕСЛИ сделаю домашку И будет хорошая погода»
- Домашка сделана (1) И погода хорошая (1) = Иду гулять (1) ✅
- Домашка не сделана (0) И погода хорошая (1) = Сижу дома (0) ❌
🔀 ИЛИ (дизъюнкция) — символ ∨ или |
Результат истинен, если истинно ХОТЯ БЫ ОДНО условие.
| A | B | A ИЛИ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Пример из жизни:
«Я буду играть в эту игру, ЕСЛИ она бесплатная ИЛИ если у меня есть деньги»
- Игра бесплатная (1) ИЛИ деньги есть (1) = Играю (1) ✅
- Игра бесплатная (1) ИЛИ денег нет (0) = Всё равно играю (1) ✅
- Игра платная (0) ИЛИ денег нет (0) = Не играю (0) ❌
🔄 НЕ (инверсия) — символ ¬ или черта сверху
Просто переворачивает значение: из истины делает ложь, из лжи — истину.
| A | НЕ A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Пример из жизни:
«Я НЕ голоден» — если «я голоден» = 1 (истина), то «я НЕ голоден» = 0 (ложь)
📋 Полная таблица обозначений
| Логическая связка | Логическая операция | Другое название | Обозначение |
|---|---|---|---|
| НЕ | Логическое отрицание | Инверсия | ¬, черта сверху |
| И | Логическое умножение | Конъюнкция | ∧, ·, & |
| ИЛИ | Логическое сложение | Дизъюнкция | ∨, +, | |
§ 2.2.3. Логические операции и операции над множествами
Сейчас покажу тебе крутую штуку: логические операции очень похожи на операции с множествами! Если помнишь круги Эйлера из математики — вот это оно и есть.
🔵 Пересечение (∩) = операция И
Пересечение двух множеств X и Y — это все элементы, которые есть И в X, И в Y одновременно.
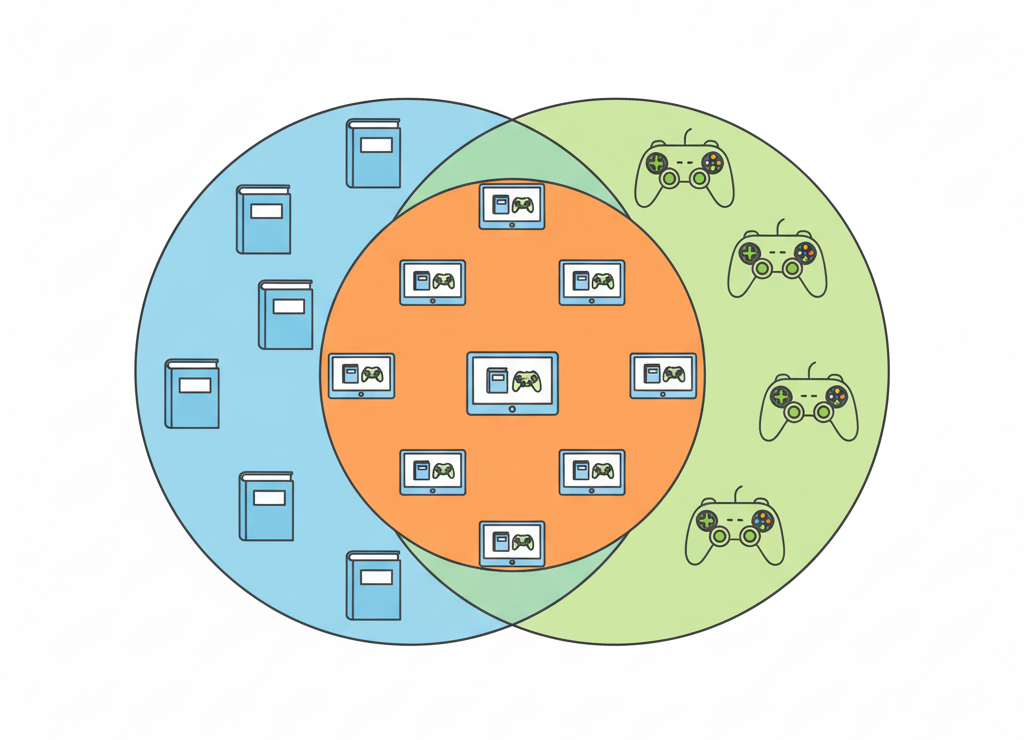
Пересечение множеств — общая часть
Пример из жизни:
- X — страницы, где встречается слово «крейсер»
- Y — страницы, где встречается слово «линкор»
- X ∩ Y — страницы, где есть ОБА слова одновременно
Это прямо как поисковик работает! Когда ты вбиваешь «крейсер И линкор», поисковик ищет пересечение множеств.
🟢 Объединение (∪) = операция ИЛИ
Объединение двух множеств X и Y — это ВСЕ элементы, которые есть хотя бы в одном из них.
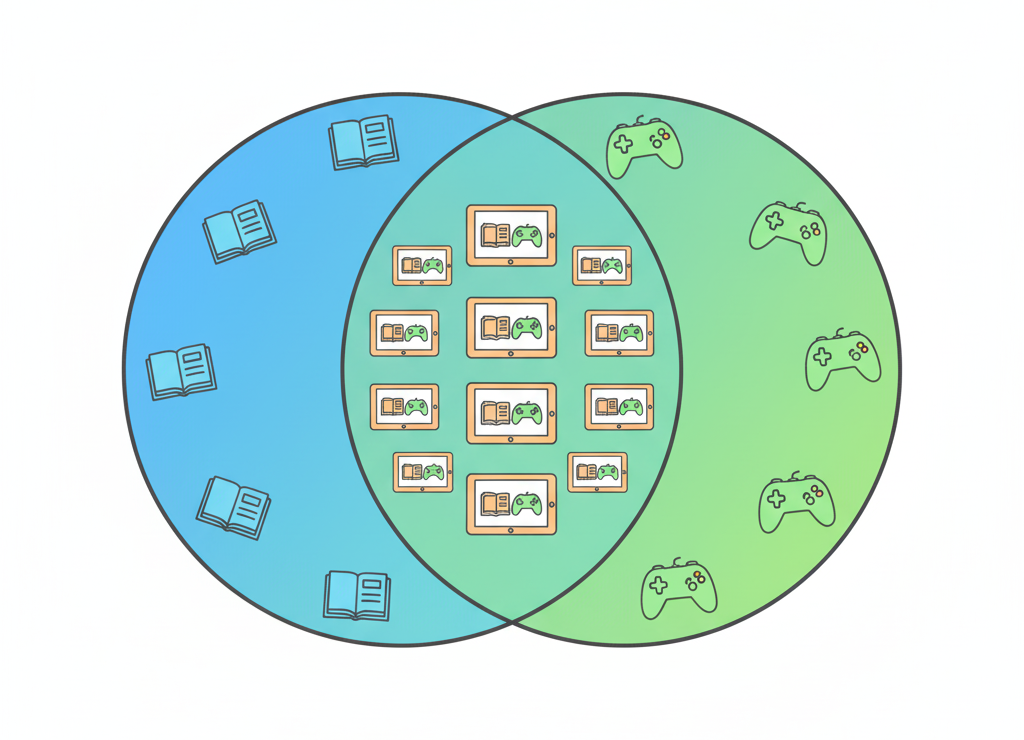
Объединение множеств — всё вместе
Пример из жизни:
- X — страницы со словом «крейсер»
- Y — страницы со словом «линкор»
- X ∪ Y — страницы, где есть ХОТЯ БЫ ОДНО из этих слов
Когда в поисковике пишешь «крейсер ИЛИ линкор» — он ищет объединение!
🔍 Практический пример из интернета
Задача: Поисковик нашёл:
- По запросу «крейсер»: 4800 страниц
- По запросу «линкор»: 4500 страниц
- По запросу «крейсер | линкор» (это ИЛИ): 7000 страниц
Вопрос: Сколько страниц найдётся по запросу «крейсер & линкор» (это И)?
💡 Решение
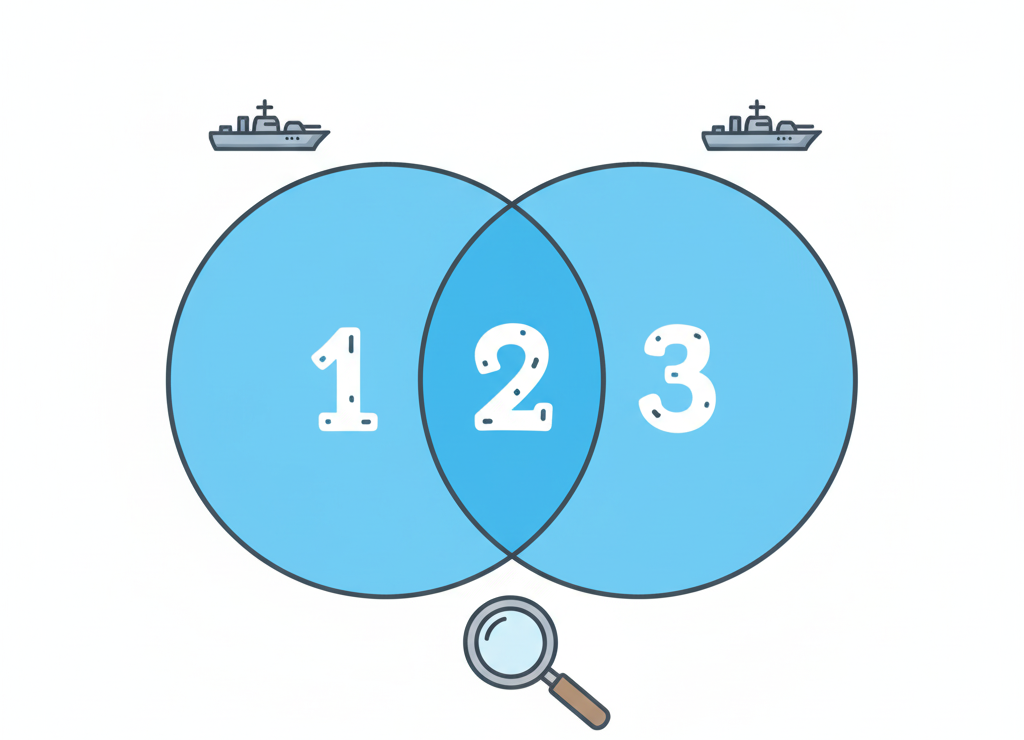
Визуальное решение задачи с поисковиком
Обозначим области:
- Область 1: только «крейсер» (без «линкор»)
- Область 2: оба слова вместе (пересечение)
- Область 3: только «линкор» (без «крейсер»)
Мы знаем:
- Область 1 + Область 2 = 4800 (все «крейсер»)
- Область 2 + Область 3 = 4500 (все «линкор»)
- Область 1 + Область 2 + Область 3 = 7000 (всё вместе)
Складываем первые два уравнения:
(Область 1 + Область 2) + (Область 2 + Область 3) = 4800 + 4500
Область 1 + 2×Область 2 + Область 3 = 9300
Но мы знаем, что Область 1 + Область 2 + Область 3 = 7000
Значит:
2×Область 2 = 9300 - 7000 = 2300
Область 2 = 2300 страниц
Ответ: По запросу «крейсер & линкор» будет найдено 2300 страниц.
§ 2.2.4. Логические выражения
Теперь мы готовы к главному — логическим выражениям!
📝 Что это такое?
Логическое выражение — это формула, составленная из:
- логических переменных (A, B, X, Y...)
- логических значений (0 и 1)
- знаков логических операций (И, ИЛИ, НЕ)
- скобок (для порядка действий)
Прямо как в алгебре, только вместо чисел — истина и ложь!
Решение логических выражений — как собирание пазла
⚠️ Порядок выполнения операций
Важно! У логических операций есть приоритет (как умножение выполняется раньше сложения):
- НЕ (инверсия) — выполняется первой
- И (конъюнкция) — выполняется второй
- ИЛИ (дизъюнкция) — выполняется третьей
Скобки меняют порядок, как обычно.
🎯 Как вычислить значение логического выражения?
Алгоритм:
- Вычисли значения в скобках (если есть)
- Выполни операции в правильном порядке: сначала НЕ, потом И, потом ИЛИ
📊 Примеры вычислений
1) (0 ∨ 1) ∧ 1 = 1 ∧ 1 = 1
- Сначала скобки: 0 ИЛИ 1 = 1
- Потом И: 1 И 1 = 1
2) ¬(0 ∨ 1 ∧ 1) = ¬(0 ∨ 1) = ¬1 = 0
- Сначала И внутри: 1 И 1 = 1
- Потом ИЛИ: 0 ИЛИ 1 = 1
- В конце НЕ: НЕ 1 = 0
3) (1 ∨ 1) ∧ (0 ∨ 1) = 1 ∧ 1 = 1
4) 1 ∨ 1 ∧ 0 ∨ 1 = 1 ∨ 0 ∨ 1 = 1
- Сначала И: 1 И 0 = 0
- Потом ИЛИ по порядку: 1 ИЛИ 0 ИЛИ 1 = 1
5) ¬(0 ∧ 1) ∧ ¬1 = ¬0 ∧ ¬1 = 1 ∧ 0 = 0
🔧 Законы операций с константами 0 и 1
Эти правила помогают упрощать сложные выражения:
- A ∨ 0 = A — если к переменной добавить ИЛИ 0, ничего не изменится
- A ∧ 0 = 0 — если умножить на 0, всегда получится 0
- A ∨ 1 = 1 — если есть хотя бы одна истина, результат истина
- A ∧ 1 = A — умножение на 1 не меняет значение
§ 2.2.5. Решение логических задач
А теперь применим всё, что узнали, для решения реальных задач!
🏅 Задача: Соревнования по гимнастике
Условие:
В соревнованиях участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения:
- Сима будет первой, Валя — второй
- Сима будет второй, Даша — третьей
- Алла будет второй, Даша — четвёртой
После соревнований выяснилось: в каждом предположении одно утверждение истинно, другое — ложно.
Вопрос: Какое место заняла каждая девушка?

Логика помогает раскрыть тайну соревнований
💡 Решение
Обозначим простые высказывания:
- C₁ = «Сима заняла первое место»
- B₂ = «Валя заняла второе место»
- C₂ = «Сима заняла второе место»
- Д₃ = «Даша заняла третье место»
- A₂ = «Алла заняла второе место»
- Д₄ = «Даша заняла четвёртое место»
Каждое предположение: одно истинно, другое ложно:
- 1) C₁ + B₂ = 1, C₁ · B₂ = 0
- 2) C₂ + Д₃ = 1, C₂ · Д₃ = 0
- 3) A₂ + Д₄ = 1, A₂ · Д₄ = 0
Логическое произведение истинных высказываний будет истинным:
(C₁ + B₂) · (C₂ + Д₃) · (A₂ + Д₄) = 1
Применяя распределительный закон и учитывая закон операций с константой 0, после преобразований получаем:
C₁ · Д₃ · A₂ = 1
Из последнего равенства следует, что C₁ = 1, Д₃ = 1, A₂ = 1
Ответ:
- Сима — 1 место
- Алла — 2 место
- Даша — 3 место
- Валя — 4 место
✨ САМОЕ ГЛАВНОЕ
Давай соберём всё, что мы узнали:
🤔 ПРОВЕРЬ СЕБЯ
Проверьте, как хорошо вы усвоили материал!
1. Определите логические переменные
Определите, какие из этих высказываний являются логическими переменными:
- а) Число 376 чётное и трёхзначное
- б) Зимой дети катаются на коньках или на лыжах
- в) Новый год мы встречаем на даче или на Красной площади
- г) Неверно, что Солнце движется вокруг Земли
- д) Земля имеет форму шара, который из космоса кажется голубым
2. Язык логики
Пусть A = «Ане нравятся уроки математики», B = «Ане нравятся уроки химии».
Выразите на разговорном языке:
- а) A ∧ B
- б) А̅ ∧ B (А с чертой сверху — это НЕ А)
- в) А̅ ∧ B̅ (оба с чертой)
3. Вычислите значения выражений
- а) (1 ∨ 1) ∨ (1 ∨ 0)
- б) (((1 ∨ 0) ∨ 1) ∨ 1)
- в) (0 ∧ 1) ∧ 1
- г) 1 ∧ (1 ∧ 1) ∧ 1
- д) ((1 ∨ 0) ∧ (1 ∧ 1)) ∧ (0 ∨ 1)
- е) ((1 ∧ 1) ∨ 0) ∧ (0 ∨ 1)
- ж) ((0 ∧ 0) ∨ 0) ∧ (1 ∨ 1)
- з) (A ∨ 1) ∨ (B ∨ 0)
- и) ((1 ∧ A) ∨ (B ∧ 0)) ∨ 1
- к) 1 ∧ A ∧ 0
4. Логические операции с именами
Пусть A = «Первая буква имени — гласная», B = «Четвёртая буква имени — согласная».
Найдите значение логического выражения A ∨ B для имён:
- ЕЛЕНА
- ВАДИМ
- АНТОН
- ФЁДОР
5. Неравенства
Пусть A = «X < 3», B = «X >= 5».
Найдите значение логического выражения А ∧ B для значений X:
- а) 2
- б) 3
- в) 4
- г) 5
- д) 6
6. Множества в фигурных скобках
Пусть M = {1, 2, 3, 4, 5, 6}, K = {1, 3, 5}, P = {2, 4, 6, 7, 8}.
Запишите в фигурных скобках области истинности следующих высказывательных форм:
- а) (x ∈ M) ∧ (x ∈ P)
- б) (x ∈ K) ∧ (x ∈ P)
- в) x ∈ M ∩ P
- г) x ∈ K ∪ P
7. Задача про поисковик
В языке запросов поискового сервера для обозначения логической операции ИЛИ используется символ «|», а для обозначения логической операции И — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| крейсер | линкор | 3700 |
| крейсер & линкор | 400 |
| линкор | 1800 |
Какое количество страниц (в тысячах) будет найдено по запросу крейсер?
8. Найдите наименьшее число
Определите наименьшее целое число X, для которого истинно высказывание: НЕ (X < 59) И НЕ (X — чётное).
9. Найдите наибольшее число
Определите наибольшее целое число X, для которого истинно высказывание: НЕ (X >= 60) И НЕ (X — нечётное).
10. Задача про древний сосуд ⚱️
Алёна, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
- Алёна: «Это сосуд греческий и изготовлен в V веке».
- Боря: «Это сосуд финикийский и изготовлен в III веке».
- Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений.
Где и в каком веке изготовлен сосуд?
🎯 Практические задания
Попробуйте применить полученные знания на практике!
✍️ Задание 1: Составьте таблицы истинности
Постройте таблицы истинности для выражений:
- A ∧ (B ∨ C)
- (A ∨ B) ∧ (A ∨ C)
- ¬A ∨ (B ∧ C)
Подсказка: определите количество строк в таблице по формуле 2ⁿ, где n — количество переменных.
🔍 Задание 2: Упростите выражения
Используя законы логики, упростите:
- A ∧ 1 ∨ B ∧ 0
- (A ∨ 0) ∧ (B ∨ 0)
- ¬(¬A ∧ ¬B)
🎨 Задание 3: Нарисуйте диаграммы
Изобразите с помощью кругов Эйлера:
- (A ∩ B) ∪ C
- A ∩ (B ∪ C)
- (A ∪ B) ∩ (A ∪ C)
Закрасьте нужные области разными цветами.
🔄 Задание 4: Придумайте свою задачу
Составьте логическую задачу про трёх друзей, где в каждом высказывании одна часть истинна, а другая ложна. Обменяйтесь задачами с одноклассниками!