Объекты алгоритмов
Привет! Сегодня мы узнаем, с чем работают алгоритмы. Какие «штуки» компьютер может обрабатывать, когда выполняет наши команды? Давайте разберёмся вместе!

Величины — это то, с чем мы работаем
Представь, что ты пишешь программу для расчёта зарплаты в какой-нибудь компании. Что тебе нужно знать? Имя сотрудника, его должность, оклад, количество отработанных часов... Все эти «кусочки информации» — это и есть объекты алгоритма.
💡 Определение
В информатике отдельный информационный объект (число, символ, строка, таблица и так далее) называется величиной.

Константы неизменны, а переменные могут меняться во время работы алгоритма
Константы и переменные
Величины делятся на два типа: постоянные (константы) и переменные.
🔒 Константа
Величина, значение которой указывается в тексте алгоритма и не меняется во время его выполнения.
Примеры из жизни:
- Количество дней в неделе (7)
- Скорость свободного падения (9,8 м/с²)
- Количество пальцев на руке (5)
🔄 Переменная
Величина, значение которой может изменяться в процессе выполнения алгоритма. При выполнении алгоритма в каждый момент времени переменная имеет текущее значение.
Примеры из жизни:
- Твой возраст (каждый год меняется)
- Количество дней в месяце (28-31)
- Пульс человека
Операции над величинами
Над величинами выполняются некоторые операции. Например:
+, −, * (умножение), / (деление)
<, >, <=, >=, =
И, ИЛИ, НЕ
⚠️ Важно!
Объекты, над которыми выполняются операции, называются операндами. Не всякий объект может быть операндом для любой операции. Например, текст не может быть объектом для арифметических операций; отрицательное число не может быть операндом для извлечения квадратного корня.
Типы величин
Множество величин, объединённых множеством допустимых значений и определённой совокупностью допустимых операций, называют величинами определённого типа.

Каждый тип величин — это свой «контейнер» с определёнными правилами
🔢 Целые и вещественные
В математике и физике оперируют числовыми величинами — натуральными, целыми, действительными числами.
В Школьном алгоритмическом языке:
- цел — целые числа
- вещ — вещественные числа
📝 Символы и тексты
В задачах повседневной жизни встречаются нечисловые величины — символы, слова, тексты.
Типы:
- сим — один символ (буква, цифра, знак)
- лит — последовательность символов (строка)
Примеры литерных значений: '2022', 'алгоритм', 'литерная величина'
💡 Истина или ложь
Величины логического (лог) типа могут принимать всего два значения:
- ДА (ИСТИНА, TRUE, 1)
- НЕЛЬЗЯ (ЛОЖЬ, FALSE, 0)
Имена величин — ярлыки на ящиках
Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр: A1, M, AP.

Имя переменной — это ярлык на ящике с данными
✨ Мнемонические имена
Рекомендуется выбирать мнемонические имена — то есть имена, отражающие суть объектов решаемой задачи.
Примеры: SUMMA, PLAN, TEMP, NUM, DEL
🎯 Пример из твоей жизни
Представь, что у тебя в комнате несколько коробок. Чтобы не путаться, ты подписываешь их: «Игры», «Книги», «Одежда». Точно так же и в программировании — переменным дают понятные имена!
Если величину представить как ящик, содержимым которого является некоторое значение, то имя величины — это ярлык, повешенный на ящик.
Выражения — вычисляем результат
Выражение — языковая конструкция для вычисления значения с использованием одного или нескольких операндов.
📝 Как записываются выражения
Выражения состоят из операндов (констант, переменных, функций), объединённых знаками операций. Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, обыкновенных дробей и так далее); знаки операций пропускать нельзя.
Порядок выполнения операций определяется скобками и приоритетом (старшинством) операций; операции одинакового приоритета выполняются слева направо.
Три типа выражений: считаем числа, проверяем условия, соединяем слова
Различают арифметические, логические и строковые выражения.
🔢 Для вычисления чисел
Арифметические выражения служат для определения числового значения.
Пример: 2 * x + 3
- При x = 1 значение равно 5
- При x = −1 значение равно 1
Функции: sqrt(x) — квадратный корень из x
Пример из жизни: Ты хочешь посчитать, сколько денег у тебя останется после похода в кино. Если билет стоит 300 рублей, попкорн — 200, а у тебя есть 1000 рублей, то выражение будет: 1000 − 300 − 200 = 500 рублей.
✔️ Для проверки условий
Логические выражения описывают некоторые условия, которые могут выполняться или не выполняться. Логическое выражение может принимать одно из двух значений — ИСТИНА или ЛОЖЬ.
Пример: (x > 5) и (x < 10)
- При x = 6 значение — ИСТИНА
- При x = 12 значение — ЛОЖЬ
Пример из жизни: Ты проверяешь, можешь ли пойти гулять. Условие: «Уроки сделаны» И «На улице не дождь». Если оба условия выполнены — ИСТИНА (можно идти), если хотя бы одно НЕТ — ЛОЖЬ (остаёшься дома).
📝 Для работы с текстом
Строковые выражения состоят из величин символьного и литерного типов, соответствующих функций и операций сцепления (присоединения).
Операция сцепления обозначается знаком «+» и позволяет соединить в одну последовательность несколько последовательностей символов.
Пример: если A = 'дом', то значение выражения 'а' + A есть 'адом'.
Пример из жизни: Ты создаёшь ник для игры. Твоё имя — «Алекс», любимое число — «777». Сцепляешь их: «Алекс» + «777» = «Алекс777».
Команда присваивания — меняем содержимое ящика
Задать конкретное значение величины можно с помощью операции присваивания, которая записывается так:
📌 Синтаксис команды присваивания
<имя переменной> := <выражение>
Знак := читается «присвоить».
Пример: A := B + 5 читается так: «переменной A присвоить значение выражения B плюс 5».

Присваивание — это как переложить значение из одной коробки в другую, стирая старое содержимое
⚠️ Важное различие!
Знаки присваивания := и равенства = — разные знаки:
- знак = означает равенство двух величин, записанных по обе стороны от этого знака
- знак := предписывает выполнение операции присваивания
Пример: запись A := A + 1 выражает не равенство значений A и A + 1, а указание увеличить значение переменной A на единицу.
Как работает присваивание?
При выполнении команды присваивания сначала вычисляется значение выражения, стоящего справа от знака :=, затем результат присваивается переменной, стоящей слева от знака :=. При этом тип выражения должен быть совместим с типом соответствующей переменной.
Пока переменной не присвоено значение, она остаётся неопределённой
Значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующего присваивания этой переменной нового значения
Если мы присваиваем некоторой переменной очередное значение, то предыдущее её значение теряется безвозвратно
📝 Пример 2: Обмен значениями
Задача: Составим алгоритм, в результате которого переменные A и B литерного типа обменяются своими значениями.
❌ Неверное решение:
A := B B := A
После выполнения первой команды первоначальное значение переменной A будет безвозвратно утрачено. В результате обе переменные получат одно и то же значение.
✅ Правильное решение:
Для поиска правильного решения воспользуемся аналогией. Если требуется перелить жидкость из сосуда 1 в сосуд 2, а из сосуда 2 — в сосуд 1, то без дополнительного сосуда 3 здесь не обойтись.
Для решения исходной задачи введём промежуточную переменную M:
нач
M := A
A := B
B := M
кон

Чтобы обменять содержимое двух сосудов, нужен третий — временный
Для числовых величин: обмен можно организовать без промежуточной переменной:
A := A + B B := A - B A := A - B
Табличные величины — когда данных много
В практической деятельности человек часто использует всевозможные таблицы. Это, например, список учащихся в классном журнале, табель успеваемости, таблица результатов спортивных соревнований и так далее. Чаще всего встречаются линейные и прямоугольные таблицы.
Линейная таблица — это один ряд данных, прямоугольная — целая сетка!
📊 Линейная таблица
Линейная таблица (одномерный массив) представляет собой набор однотипных данных, записанных в одну строку или один столбец. Элементы строки (столбца) всегда нумеруются.
Примеры использования:
- Дни недели
- Количество пропущенных уроков за неделю
📋 Прямоугольная таблица
Прямоугольная таблица (двумерный массив) — это упорядоченный некоторым образом набор строк (столбцов), содержащих одинаковое количество элементов. Строки прямоугольных таблиц имеют свою нумерацию, столбцы — свою.
Примеры использования:
- Количество уроков, пропущенных всеми учениками класса за неделю
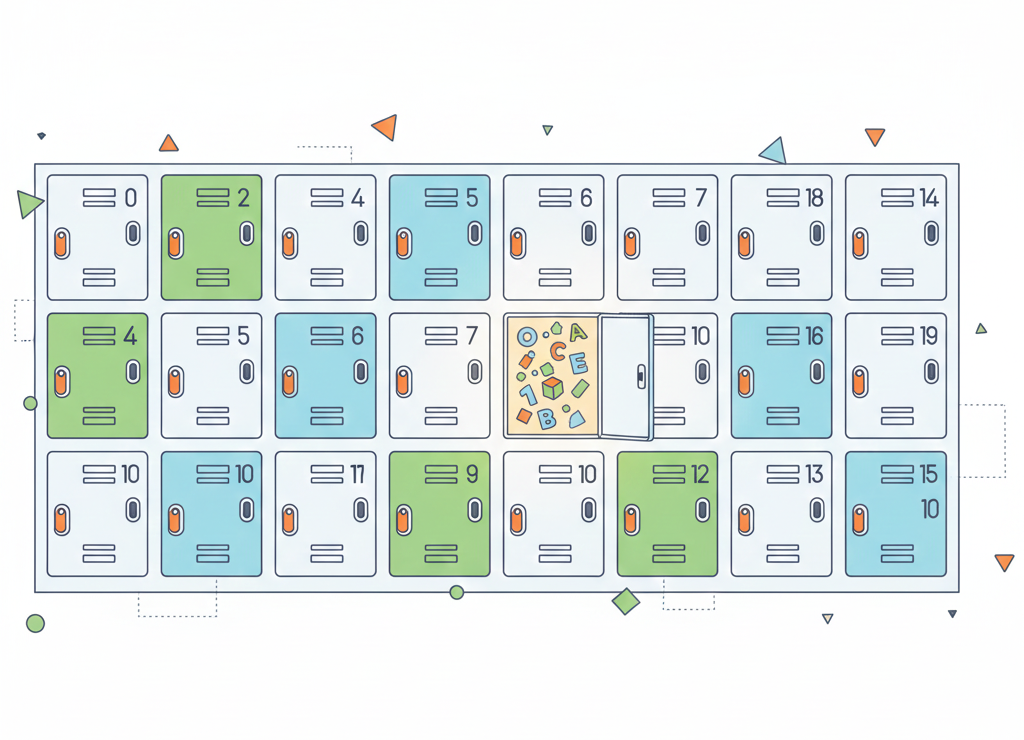
Индексы — это номера ячеек, по которым мы находим нужные данные
🔢 Как работать с таблицами
Всей совокупности элементов табличной величины даётся одно имя. Элементы различают по их номерам, называемым индексами. Индексы записываются в квадратных скобках сразу за именем таблицы.
Пример с линейной таблицей WEEK:
- WEEK[1] = 'Понедельник'
- WEEK[6] = 'Суббота'
Пример с прямоугольной таблицей LES:
В этой таблице положение элемента задаётся двумя индексами: номером строки и номером столбца.
- LES[1, 1] = 6
- LES[2, 5] = 6
- LES[3, 4] = 0
🎯 Аналогия из жизни
Линейные и прямоугольные таблицы наглядно можно представить как аналоги привычных нам объектов — рядов шкафчиков в раздевалках, почтовых ящиков, ячеек для хранения сумок в супермаркетах.
🎯 Самое главное
Давай подытожим всё, что мы узнали:
🤔 Проверь себя
Теперь давай проверим, как ты усвоил материал! Попробуй ответить на эти вопросы. Не спеши — подумай!
1. Что такое величина? Чем различаются постоянные и переменные величины?
Попробуй объяснить это на своих примерах!
2. Величины каких типов используются при записи алгоритмов?
Вспомни: числовые, символьные, логические...
3. Укажи тип величины, если её значение равно: 2022; 14.48; 'ДА'; FALSE; −125; '142'; 1,4 · 10²; .123E−2; 'ЛОЖЬ'
Обращай внимание на кавычки и форму записи!
4. Определи типы следующих величин: а) вес человека; б) марка автомобиля; в) год вашего рождения; г) площадь фигуры; д) название месяца года; е) количество мест в самолёте
Подумай, какой тип данных подходит для каждого случая.
5. Работая в группе, приведите примеры допустимых и недопустимых значений для величин: температура человека, скорость автомашины, площадь страны, название дня недели
Обсудите, что реально, а что — нет!
6. Для чего предназначена команда присваивания? Каковы её основные свойства?
Вспомни пример с ящиками!
7. Какая команда присваивания составлена правильно? а) A := B; б) A = B; в) A = B − 1; г) A + 1 := A
Знак := — это всегда присваивание!
8. Придумайте свой алгоритм обмена значениями числовых переменных A и B
Можешь использовать третью переменную или математические операции!
9. Имеются числовые переменные A, B и C. Сколько промежуточных переменных потребуется, чтобы A получило значение B, B — значение C, а C — значение A? Запишите алгоритм
Это головоломка! Представь, как передать три предмета по кругу.
10. После выполнения команды x := x ⦁ y значение x равно 3, а y равно 5. Чему были равны x и y ДО выполнения команды?
Работай в обратном направлении!
11. Что называют выражением? Каковы основные правила записи выражений?
Вспомни про операнды, операции, скобки и приоритеты.
12. Переведите выражение из линейной записи на языке математики: a * b / c; a / b * c; a + b / c; (a + b) / c; a + b / c + a; (a + b) / (c − a)
Помни о порядке операций и скобках!
13. Запишите на Школьном алгоритмическом языке: ax² + bx + c; v₀ + (at²)/2; (1/2)(a+b)h; (1+x₁x₂)/(b²c); √(a²+b²)
Всё пишется в одну строку, используй скобки!
14. Запишите логическое выражение, истинное при выполнении условия: а) x принадлежит отрезку [0, 1]; б) x лежит вне отрезка [0, 1]; в) каждое из x, y положительно; г) хотя бы одно из x, y положительно; д) ни одно из x, y не положительно; е) только одно из x, y положительно
Используй операции И, ИЛИ, НЕ, операции сравнения.
15. Изобразите в декартовой системе координат область, где истинно: а) (x >= −1) И (x <= 1) И (y >= −1) И (y <= 1); б) (y >= x) И (y >= −x) И (y <= 1)
Нарисуй координатную плоскость и заштрихуй нужную область!
16. Запишите логическое выражение, принимающее значение TRUE, когда точка (x, y) принадлежит закрашенной области на рисунке
Определи границы области и запиши условия.
17. Запишите команду присваивания, где логическая переменная t получает TRUE, если выполняется условие: а) x — положительное число; б) хотя бы одно из x, y, z равно нулю; в) числа x, y, z равны между собой
Формат: t := (условие)
18. Какие величины целесообразно представлять с помощью таблиц? Список: учеников класса, рост учеников, средний рост, оценка по физике, средний балл, оценки за контрольную, длины сторон треугольника, длины нескольких треугольников, дни недели, имя человека, площадь фигуры, периметры треугольников, температура января, количество девочек, дождливая декада
Обсудите в группе: когда нужна таблица, а когда — одна величина?