Конструирование алгоритмов
Привет! Сегодня мы разберём, как создавать алгоритмы — те самые пошаговые инструкции, которые управляют всем: от твоего смартфона до беспилотников. Звучит сложно? На самом деле ты уже каждый день пользуешься алгоритмами, даже не замечая этого!

🎯 Зачем нам это нужно?
Представь: ты хочешь научить друга проходить сложный уровень в игре. Ты не можешь просто сказать «пройди его» — нужна чёткая инструкция: куда идти, что нажимать, когда прыгать. Вот это и есть алгоритм!
В программировании то же самое: компьютер — твой «друг», который знает только то, что ты ему объяснишь. И объяснить надо так, чтобы не осталось ни одного непонятного момента.
1.1.1 Методы построения алгоритмов
В 8 классе вы уже познакомились с базовыми алгоритмическими конструкциями: следованием, ветвлением и циклом. Вы научились записывать несложные алгоритмы на одном из языков программирования. Отлично! Теперь поднимемся на уровень выше.
Как рождается алгоритм?
Когда перед тобой стоит сложная задача, её нужно разбить на более простые подзадачи. Это как собирать LEGO: сначала делаешь отдельные блоки, потом соединяешь их в крутую модель.
Обычно используют один из двух подходов:
🔹 Метод «сверху вниз» (пошаговая детализация)
Это как планирование путешествия:
- Сначала общий план: «Хочу поехать в другой город»
- Потом детали: «Куплю билет на поезд»
- Ещё детальнее: «Зайду на сайт РЖД, выберу дату, оплачу картой»
Пример из жизни: Представь, что ты объясняешь роботу, как приготовить бутерброд. Нельзя просто сказать «сделай бутерброд» — нужно: возьми хлеб, открой холодильник, достань масло, намажь хлеб, положи сыр... и так далее.
🔹 Метод «снизу вверх»
Это когда у тебя уже есть готовые «кирпичики» — небольшие алгоритмы, которые решают простые задачи. Ты берёшь их и комбинируешь, создавая что-то более сложное.
Пример из жизни: В видеоиграх есть готовые блоки: «прыжок», «удар», «бег». Разработчики комбинируют их, создавая комбо-атаки и сложные движения персонажа.
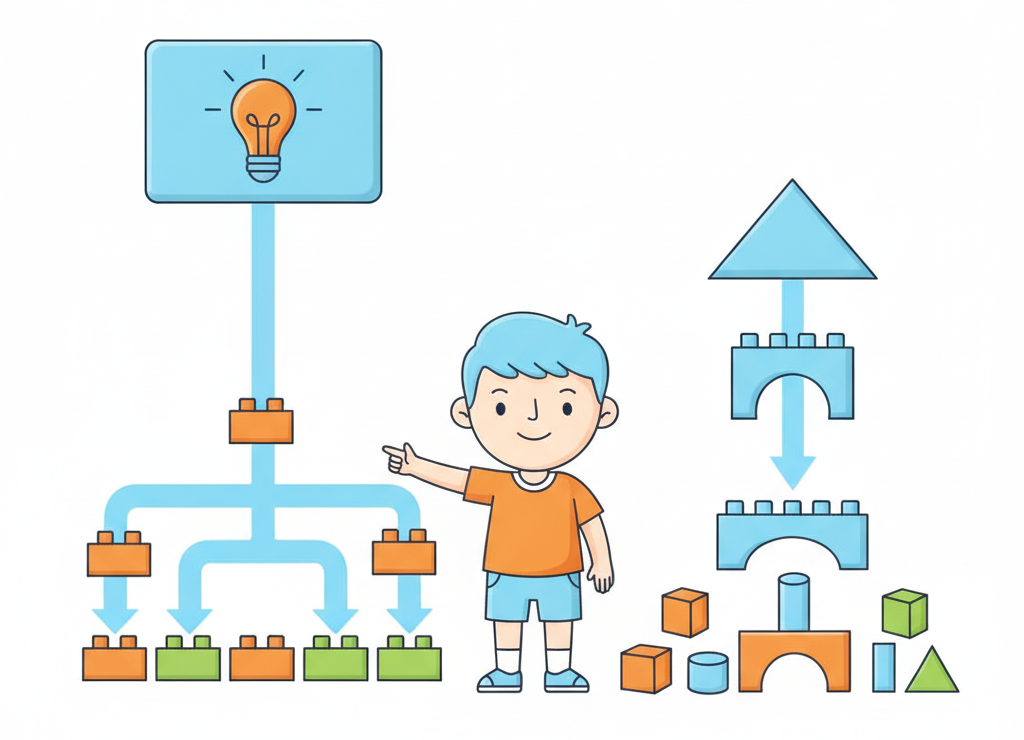
Два пути к созданию алгоритма: разбиваем сложное на простое или собираем простое в сложное
1.1.2 Разработка алгоритма методом пошаговой детализации для исполнителя Робот
Помнишь исполнителя Робот? Он живёт на клетчатом поле, может двигаться между клетками и закрашивать их. Ничего лишнего — простой, но очень полезный помощник для понимания алгоритмов.
Система команд Робота:
| Команда | Описание команды |
|---|---|
| Вверх | Робот перемещается в соседнюю клетку в указанном направлении. Если в этом направлении между клетками стоит стена, то Робот разрушается |
| Вниз | |
| Вправо | |
| Влево | |
| Закрасить | Робот закрашивает ту клетку, в которой находится |
| Сверху свободно | Проверка истинности условия отсутствия стены у соответствующей стороны той клетки, где находится Робот: стены нет — «истина», иначе «ложь» |
| Снизу свободно | |
| Слева свободно | |
| Справа свободно | |
| Сверху стена | Проверка истинности условия наличия стены у соответствующей стороны той клетки, где находится Робот: стена есть — «истина», иначе «ложь» |
| Снизу стена | |
| Слева стена | |
| Справа стена | |
| Клетка закрашена | Проверка истинности условия: клетка закрашена — «истина», иначе «ложь» |
| если <условие> то <команда 1> иначе <команда 2> все |
Организация ветвления: если <условие> истинно, то выполняется <команда 1>; если <условие> ложно, то выполняется <команда 2> |
| нц пока <условие> <последовательность команд> кц |
Организация цикла: пока <условие> истинно, выполняется <последовательность команд> |
Важно: В одном условии можно использовать несколько команд, применяя логические операции и, или, не.
Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.
Задача: Закрасить все клетки коридора
Исходное положение Робота (отмечено ромбом)
Задача: Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.
План действий (модули):

План действий Робота (5 модулей)
Закраска всех клеток коридора левее исходной
Возвращение в исходное положение
Закраска всех клеток коридора правее исходной
Возвращение в исходное положение
Закраска исходной клетки
Детализируем каждый из пяти модулей
1️⃣ Модуль 1: Закраска клеток слева
Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:
влево
нц пока сверху стена и снизу стена
закрасить; влево
кцПод управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется в клетке левее коридора.
2️⃣ Модуль 2: Возвращение в исходную клетку
Командой вправо вернём Робота в коридор. Эта клетка — первая незакрашенная клетка, находящаяся правее Робота. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо:
вправо
нц пока клетка закрашена
вправо
кц3️⃣ Модуль 3: Закраска клеток справа
Выполнив команду вправо, Робот пройдёт исходную клетку и займёт клетку правее исходной. Теперь можно закрашивать клетки коридора, расположенные правее исходной:
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц4️⃣ Модуль 4: Возвращение в исходную клетку (повторно)
Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор:
влево
нц пока клетка закрашена
влево
кц5️⃣ Модуль 5: Закраска исходной клетки
По команде закрасить Робот закрашивает исходную клетку.
Полностью программа управления Роботом
использовать Робот
алг
нач
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц
вправо
нц пока клетка закрашена
вправо
кц
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц
влево
нц пока клетка закрашена
влево
кц
закрасить
кон💡 Проверь себя
Задание 1: Выполни приведённый выше алгоритм в среде КуМир, предварительно создав в ней стартовую обстановку — горизонтальный коридор.
Задание 2: Разработай алгоритм решения исходной задачи при условии, что в системе команд Робота отсутствуют следующие команды:
- сверху стена
- снизу стена
- слева стена
- справа стена
Модифицируй алгоритм таким образом, чтобы с его помощью можно было бы решить аналогичную задачу в вертикальном коридоре. Убедись в работоспособности разработанного алгоритма.
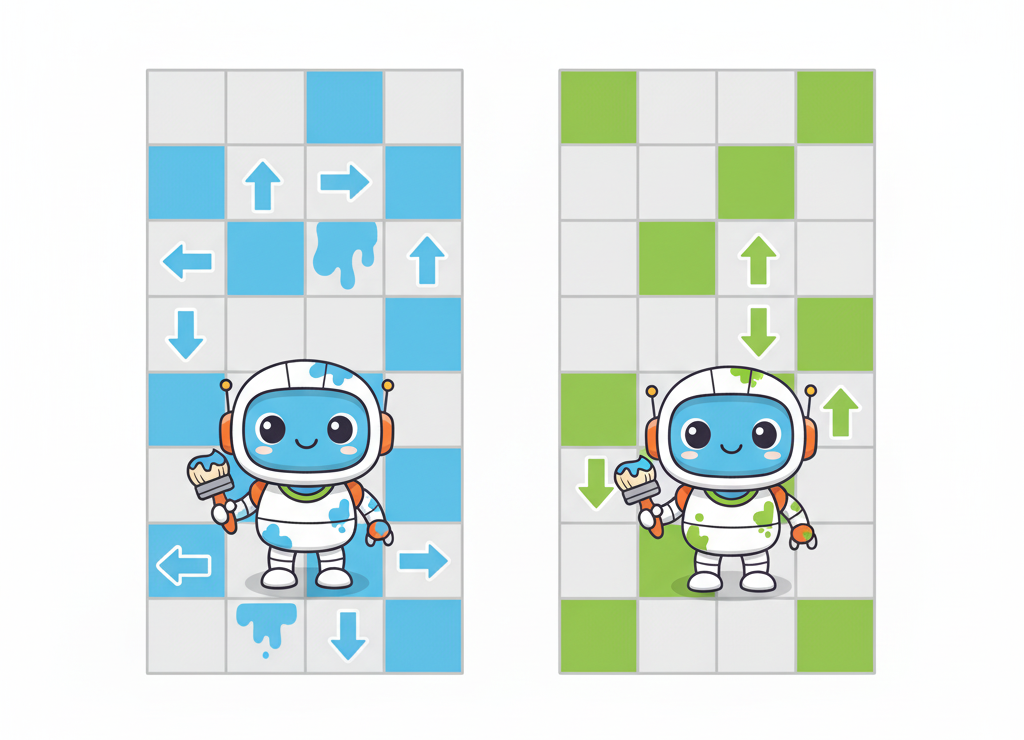
Один алгоритм, два применения: горизонтальный и вертикальный коридоры
1.1.3 Вспомогательные алгоритмы
Во многих случаях при разработке алгоритмов решения сложных задач используют вспомогательные алгоритмы. Например, это удобно, когда в разных местах алгоритма необходимо выполнение одной и той же последовательности действий.
📖 Определение
Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма для решения некоторой подзадачи основной задачи.
Такую последовательность действий оформляют отдельным алгоритмом, который вызывают в нужных местах основного алгоритма. Один и тот же вспомогательный алгоритм может использоваться в разных программах. Вспомогательные алгоритмы делают более понятной структуру основного алгоритма.
Пример 1: Рисуем узор с помощью Робота
В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого будет нарисован узор.

Узор с повторяющейся фигурой
Можно написать одну длинную программу, выполнив которую Робот закрасит все клетки, образующие этот узор. Но можно поступить иначе, обратив внимание на то, что в узоре трижды повторяется изображение одной и той же фигуры.
Разработав вспомогательный алгоритм для изображения этой фигуры, его можно вызвать нужное количество раз для построения требуемого узора.
Вспомогательный алгоритм «фигура»:
использовать Робот
алг узор
нач
фигура
вправо; вниз
фигура
вправо; вверх
фигура
кон
алг фигура
нач
закрасить; вниз
закрасить; вправо; закрасить; вверх; закрасить
кон✍️ Задание
Выполни приведённый выше алгоритм в среде КуМир. Модифицируй алгоритм таким образом, чтобы с его помощью можно было бы продолжить узор, дополнив его по горизонтали несколькими повторяющимися фигурами. Убедись в работоспособности разработанного алгоритма.
Параметры вспомогательного алгоритма
Каждый вспомогательный алгоритм получает уникальное имя, после которого указываются параметры алгоритма (при наличии) — имена переменных, обозначающих исходные данные (аргументы) и результаты вспомогательного алгоритма.
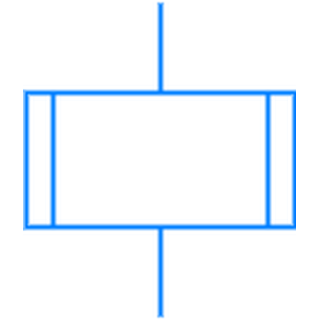
Рис 1.2. Блок «предопределённый процесс»
При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс», внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — аргументы и результаты.
Имя рассмотренного выше вспомогательного алгоритма — фигура; это вспомогательный алгоритм без параметров.
Пример 2: Черепаха рисует многоугольник
Исполнитель Черепаха перемещается на экране компьютера в квадратном окне со стороной 500 пикселей и может рисовать кончиком хвоста, оставляя след в виде линии.
Исходное положение: Черепаха находится в центре окна, хвост опущен, направление — строго вверх.
Система команд исполнителя Черепаха:
| Команда | Описание команды |
|---|---|
| поднять хвост | Последующие перемещения не оставляют след в окне на экране |
| опустить хвост | Последующие перемещения оставляют след в окне на экране |
| вперед (n) назад (n) |
Перемещение Черепахи на n шагов в направлении движения (в противоположном направлении движения); n — вещественное число |
| вправо (m) влево (m) |
Изменение направления движения Черепахи на m градусов по часовой стрелке (против часовой стрелки); m — вещественное число |
| нц k раз <последовательность команд> кц |
Черепаха повторяет k раз последовательность команд в скобках |
Выясним, что получится в результате исполнения Черепахой следующего алгоритма:
нач
нц 8 раз
вперед (50)
нц 3 раз
вперед (50)
вправо (120)
кц
назад (50)
вправо (45)
кц
кон🤔 Подумай!
В этой программе два цикла, один из которых находится внутри другого. Вспомните, как называется такая конструкция.
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.

Черепаха + циклы = удивительные узоры
✍️ Задание
Проверьте своё предположение, выполнив рассмотренный алгоритм в среде КуМир.
Оформите внутренний цикл в виде вспомогательного алгоритма без параметров треугольник. Убедитесь, что всё работает верно.
Модифицируем алгоритм с параметрами
Можно модифицировать вспомогательный алгоритм треугольник во вспомогательный алгоритм с параметрами:
многоугольник (k, n), где:
- k — количество углов основной фигуры
- n — длина стороны правильного многоугольника
алг многоугольник (арг цел k, n)
нач
нц k раз
вперед (n)
вправо (360/k)
кц
конПример 3: Находим первый простой делитель числа
Как известно, натуральные числа, большие единицы, в зависимости от количества их делителей подразделяются на простые и составные:
🔢 Простое число
Это натуральное число, большее единицы, которое делится только на единицу и само на себя
🔢 Составное число
Это натуральное число, большее единицы, которое делится не только на единицу и само на себя, но и ещё хотя бы на одно натуральное число
На уроках математики вы неоднократно выполняли разложение натурального числа a на простые множители, скорее всего действуя так: находили p — первый простой делитель числа a (самое маленькое простое число, на которое данное число a делится без остатка) и делили на него число a; находили первый простой делитель для полученного частного и делили частное на этот простой делитель и т. д., пока частное не становилось равным 1.
Алгоритм нахождения первого простого делителя:
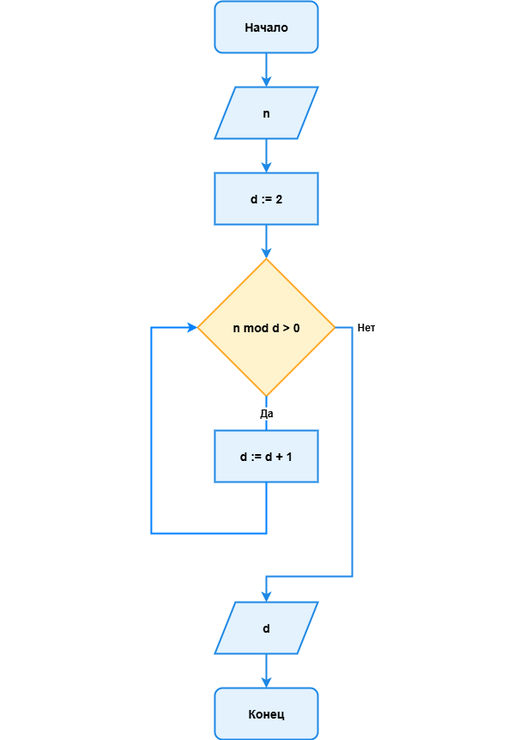
Рис 1.3. Алгоритм нахождения первого простого делителя
✍️ Задание
Попытайтесь самостоятельно записать алгоритм нахождения первого простого делителя, представленный на Рис 1.3, на известном вам языке программирования. Протестируйте свою программу на числах 121, 135 и 847. Если программа написана правильно, то результатами её выполнения будут числа 11, 5 и 7 соответственно.
Алгоритм разложения натурального числа на простые множители
Алгоритм нахождения первого простого делителя можно рассматривать как вспомогательный при решении задачи разложения натурального числа на простые множители (Рис 1.4).
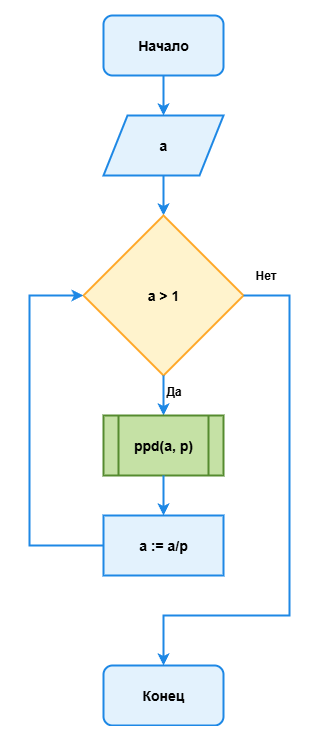
Рис 1.4. Алгоритм разложения натурального числа на простые множители
Как работает вспомогательный алгоритм ppd
Вспомогательный алгоритм нахождения первого простого делителя для некоторого числа мы назвали ppd. Его формальными параметрами являются переменные n, d; фактическими — a, p.
В общем случае команда вызова вспомогательного алгоритма исполняется следующим образом (Рис 1.5):
Формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма
Для заданных входных данных исполняются команды вспомогательного алгоритма
Полученные результаты присваиваются переменным с именами фактических результатов
Осуществляется переход к следующей команде основного алгоритма
Рис 1.5. Схема выполнения команды вызова вспомогательного алгоритма
Имена и типы переменных, которые заявлены в качестве формальных параметров, объявляются внутри вспомогательного алгоритма по тем же правилам, что и для основного алгоритма. Такие переменные называются локальными. При необходимости работать с переменными и в основном алгоритме, и во вспомогательном их объявляют как глобальные.
1.1.4 Рекурсивные алгоритмы
А теперь познакомимся с чем-то действительно крутым — рекурсией! Звучит загадочно? На самом деле ты уже встречал рекурсию в жизни, просто не знал, как это называется.
Что такое рекурсия простыми словами?
Представь, что ты стоишь между двух зеркал. Ты видишь своё отражение, в котором видно отражение отражения, в котором видно отражение отражения отражения... и так до бесконечности. Вот это и есть рекурсия — когда что-то ссылается само на себя!
📖 Определение
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Пример 4: Возведение в степень
Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа a можно представить в виде рекурсивного (Рис 1.6).
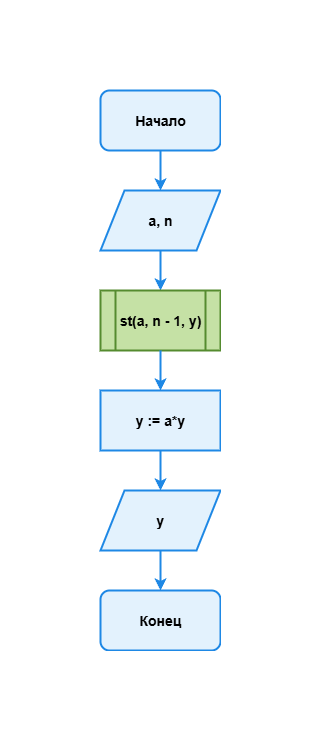
Рис 1.6. Рекурсивный алгоритм возведения в степень
Как это работает?
Число a в степени n (n-я степень числа a) есть не что иное, как произведение an-1 · a; в свою очередь, an-1 = an-2 · a и т. д.
Другими словами:
- 5³ = 5² × 5
- 5² = 5¹ × 5
- 5¹ = 5⁰ × 5
- 5⁰ = 1
Каждый раз задача упрощается, пока не дойдём до самого простого случая.
Пример 5: Ханойская башня
Рекурсивный алгоритм положен в основу эффективного решения головоломки «Ханойская башня» (Рис 1.7).

Рис 1.7. Головоломка «Ханойская башня»
В сети Интернет размещено много разных онлайн-вариантов игры «Ханойская башня». Подберите какой-нибудь из них по своему вкусу и попытайтесь решить головоломку для восьми колец за минимально возможное количество ходов. При возникновении трудностей загляните в главу 3: подсказка содержится в задании 6 для практических работ.
Суть головоломки:
Есть три стержня и несколько дисков разного размера, которые можно надевать на любой стержень. Все диски в начале игры находятся на одном из стержней, упорядоченные по размеру: самый большой внизу, самый маленький — вверху.
🎯 Цель игры:
Переместить все диски на другой стержень
📋 Правила:
- За один ход можно переместить только один диск
- Нельзя класть больший диск на меньший
- Можно использовать вспомогательный стержень
Пример 6: Снежинка Коха
Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на Рис 1.8.
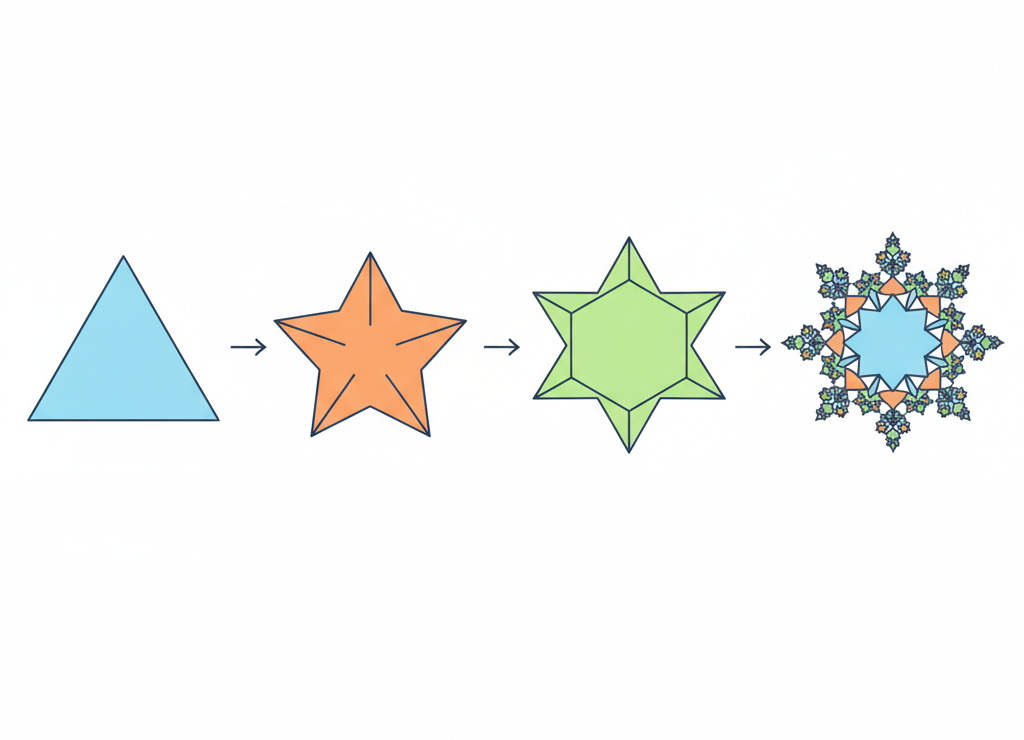
Рис 1.8. Шаги алгоритма построения снежинки Коха
С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Как это связано с жизнью?
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.
Такие фигуры называются фракталами — они встречаются в природеповсюду: в форме листьев папоротника, в структуре снежинок, в береговых линиях, в кровеносных сосудах. Даже дерево бронхов в наших лёгких — это фрактал!
А ещё фракталы активно используются в компьютерной графике для создания реалистичных пейзажей в играх и фильмах.

Фракталы: от природы к компьютеру
🎯 САМОЕ ГЛАВНОЕ
Давай закрепим то, что мы узнали:
❓ Вопросы и задания
Проверь себя:
1. Почему при решении сложной задачи затруднительно сразу конкретизировать все необходимые действия? Обсудите этот вопрос в группе.
Подсказка: Вспомни, как ты собираешься на вечеринку. Сначала думаешь «надо подготовиться», потом — «выбрать одежду, причесаться, взять подарок», а уже потом детализируешь каждый пункт. Сразу представить все шаги невозможно!
2. В чём заключается метод пошаговой детализации при построении алгоритма?
Своими словами: Это когда ты большую задачу режешь на кусочки, как пиццу. Сначала общий план, потом каждый кусок разбиваешь на ещё меньшие, пока не получишь совсем простые действия.
3. Какая связь между методом разработки алгоритма «сверху вниз» и такими процессами, как написание сочинения или подготовка к многодневному туристическому походу?
Подумай: Когда пишешь сочинение, сначала придумываешь тему, потом план из трёх частей (вступление, основная часть, заключение), а затем детализируешь каждую часть. С походом то же самое: сначала «идём в поход», потом «собираем вещи, планируем маршрут, готовим еду», а уже потом конкретные действия для каждого пункта.
4. Известен рост каждого из n учеников 9 «А» класса и m учеников 9 «В» класса. Опишите укрупнёнными блоками алгоритм сравнения среднего роста учеников этих классов.
Подсказка: Нужно три блока:
- Блок 1: посчитать средний рост для 9 «А»
- Блок 2: посчитать средний рост для 9 «В»
- Блок 3: сравнить два получившихся числа
5. На бесконечном поле имеется стена, состоящая из двух горизонтальных и одного вертикального участков. Робот находится в клетке под левой горизонтальной частью стены. Задача Робота — закрасить клетки, примыкающие сверху к горизонтальным участкам стены.
Есть план действий Робота:
- Двигаться вверх до горизонтального участка стены
- Двигаться влево под горизонтальным участком стены и сместиться на 1 клетку левее стены
- Занять положение над горизонтальным участком стены
- Закрасить клетки слева направо над горизонтальным участком стены
- Спуститься вниз вдоль вертикального участка стены
- Закрасить клетки слева направо над горизонтальным участком стены
Реализуйте этот план, составив алгоритм для Робота в среде КуМир.
6. В ряду из десяти клеток правее Робота некоторые клетки закрашены. Составьте алгоритм, который закрашивает клетки, примыкающие сверху и снизу к каждой закрашенной клетке.
Проверьте работу алгоритма в разных случаях расположения закрашенных клеток.
7. Для чего нужны вспомогательные алгоритмы? Опишите процесс выполнения команды вызова вспомогательного алгоритма в основном алгоритме.
Простой ответ: Вспомогательные алгоритмы — это как кнопки на пульте. Нажал одну кнопку «включить Netflix» — и выполнилась целая цепочка действий. Не надо каждый раз прописывать все шаги заново!
8. Составьте алгоритмы, под управлением которых Робот закрасит указанные клетки. Используйте вспомогательный алгоритм.
Попробуйте найти повторяющийся паттерн в закрашиваемых клетках и оформите его как вспомогательный алгоритм.
9. Сталкивались ли вы с идеей формальных и фактических параметров при изучении математики и физики? Приведите пример.
Подумай: В физике формула S = v·t — это как формальные параметры. Когда подставляешь конкретные значения S = 60·2, это уже фактические параметры!
10. Для исполнителя Чертёжник в среде КуМир составьте алгоритмы рисования ромбов с вложенными ромбами.
Используйте вспомогательный алгоритм для рисования одного ромба, а затем вызывайте его несколько раз с разными параметрами.
11. Какие алгоритмы называют рекурсивными? Приведите пример рекурсии из жизни.
Примеры из жизни:
- Когда ищешь что-то в куче вещей: «Посмотрю в эту коробку → О, там ещё коробка → Посмотрю в неё → О, там ещё одна...»
- Когда объясняешь другу значение слова, используя это же слово: «Рекурсия — это когда функция вызывает рекурсию» 😄
- Эффект двух зеркал, стоящих напротив
- Матрёшка — в большой куколке маленькая, в маленькой — ещё меньше...
12. В среде КуМир исследуйте алгоритм для Черепахи, содержащий рекурсию. Что получится при изменении значений параметра а?
Добавьте параметр k — количество углов основной фигуры. Предложите свои варианты рисунков для Черепахи, которые можно получить с помощью рекурсии.
использовать Черепаха
алг чертеж (цел а)
нач
если а < -150
то стоп
все
нц 4 раз
вперед (а); вправо (90)
кц
чертеж (а-5)
кон🎯 Практические задания
Попробуй применить полученные знания на практике!
💻 Задание 1: Робот в КуМире
Выполните приведённый в уроке алгоритм закрашивания коридора в среде КуМир. Создайте:
- Горизонтальный коридор разной длины
- Вертикальный коридор
- Коридор с изгибом
🎨 Задание 2: Узоры Черепахи
Создайте в КуМире программу для Черепахи, которая рисует:
- Квадрат
- Треугольник
- Многоугольник с параметром n (количество углов)
- Узор из повторяющихся фигур
🔢 Задание 3: Первый простой делитель
Напишите программу нахождения первого простого делителя числа. Протестируйте её на числах:
- 121 (ответ: 11)
- 135 (ответ: 5)
- 847 (ответ: 7)
🌀 Задание 4: Рекурсия
Исследуйте рекурсивный алгоритм для Черепахи:
- Измените начальное значение параметра а
- Измените шаг уменьшения (вместо -5)
- Добавьте параметр для количества углов
- Создайте свой рекурсивный узор

Черепаха и рекурсия — бесконечная красота в коде
📚 Дополнительные материалы
🎮 Интерактивные задачи
Попробуйте решить головоломку «Ханойская башня» онлайн. Начните с 3 дисков, затем попробуйте 5, 8 дисков.
Вопрос: Сколько минимальных ходов нужно для n дисков? Попробуйте найти закономерность!
🌟 Фракталы вокруг нас
Найдите примеры фракталов в природе:
- Сфотографируйте дерево и покажите, как ветви повторяют форму всего дерева
- Рассмотрите лист папоротника
- Изучите структуру снежинки
- Найдите береговую линию на карте