Отношения объектов и их множеств
Привет! Ты уже умеешь описывать признаки объектов — их свойства, действия, характеристики. А сегодня научишься рассказывать о том, как объекты связаны друг с другом! Это как ниточки между точками — они показывают, кто с кем дружит, что из чего состоит и многое другое. Готов? Поехали!

Что такое отношения?
Отношение — это связь между объектами. Представь, что объекты — это точки, а отношения — это ниточки, которые их соединяют.
Примеры отношений из жизни
- Иван — сын Андрея (семейное отношение)
- Эверест выше Эльбруса (сравнение)
- Винни-Пух дружит с Пятачком (дружба)
- 21 кратно 3 (математическое отношение)
- Один байт равен восьми битам (информационное равенство)
- Текстовый процессор входит в состав программного обеспечения (часть целого)
Обрати внимание!
В каждом предложении выделенное слово — это имя отношения. Оно показывает, как именно связаны объекты.
Схемы отношений — рисуем связи!
Когда объектов много и связей между ними тоже много, словами описывать их долго и запутанно. Поэтому мы рисуем схемы отношений!
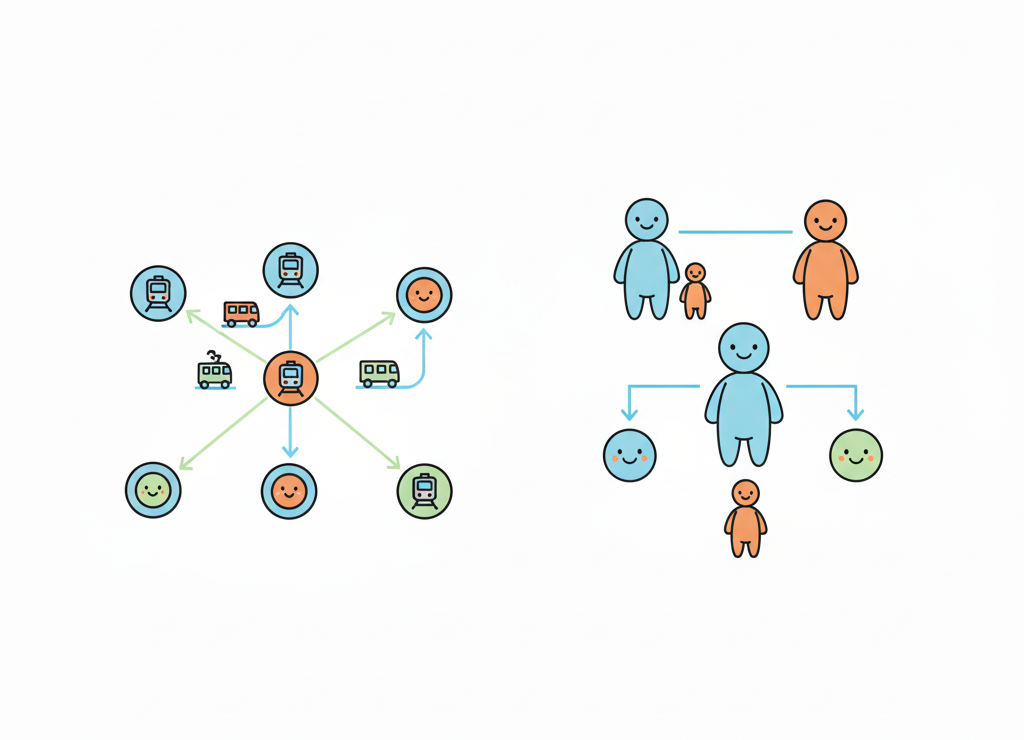
Схема отношений помогает быстро понять связи между объектами
Пример: Города и железные дороги
Представь: есть города А, Б, В, Г, Д и Е. Некоторые соединены железной дорогой:
- Город А соединён с городами В, Г и Е
- Город Е соединён с городами А, В, Г и Д
Если нарисовать это на схеме, всё станет понятно сразу! Города изображаем кружками или точками, а железные дороги — линиями между ними.
Когда нужны стрелки?
Иногда важно показать направление отношения. Например:
- «Андрей — отец Ивана» (стрелка от Андрея к Ивану)
- «Иван — сын Андрея» (стрелка от Ивана к Андрею)
Видишь? Когда меняем местами объекты, меняется и имя отношения!
Примеры изменяющихся отношений
- выше ↔ ниже
- покупает ↔ продаёт
- учит ↔ учится у
- приходится отцом ↔ приходится сыном
Лайфхак: обходимся без стрелок!
Можно придумать правило расположения объектов на схеме. Например, детей всегда рисовать ниже родителей — тогда и так понятно, кто чей отец!
Особые отношения: «является элементом множества»
Некоторые отношения работают только с определёнными типами объектов, а некоторые — со всеми!
Отношения для определённых объектов
- «лечит» — только врач может лечить пациента
- «покупает» — нужны покупатель и товар
- «соединён железной дорогой» — только для населённых пунктов
Универсальные отношения
Эти отношения могут связывать любые объекты:
- «является элементом множества»
- «входит в состав»
- «является разновидностью»
Примеры отношения «является элементом множества»
- Гарри Поттер — литературный персонаж (Гарри Поттер является элементом множества литературных персонажей)
- Камчатка — полуостров (Камчатка является элементом множества полуостровов)
- Москва — столичный город (Москва является элементом множества столичных городов)
Круги Эйлера: когда множества встречаются!
Математик Леонард Эйлер придумал изображать множества в виде кругов. Это очень удобно для понимания, как множества связаны друг с другом!
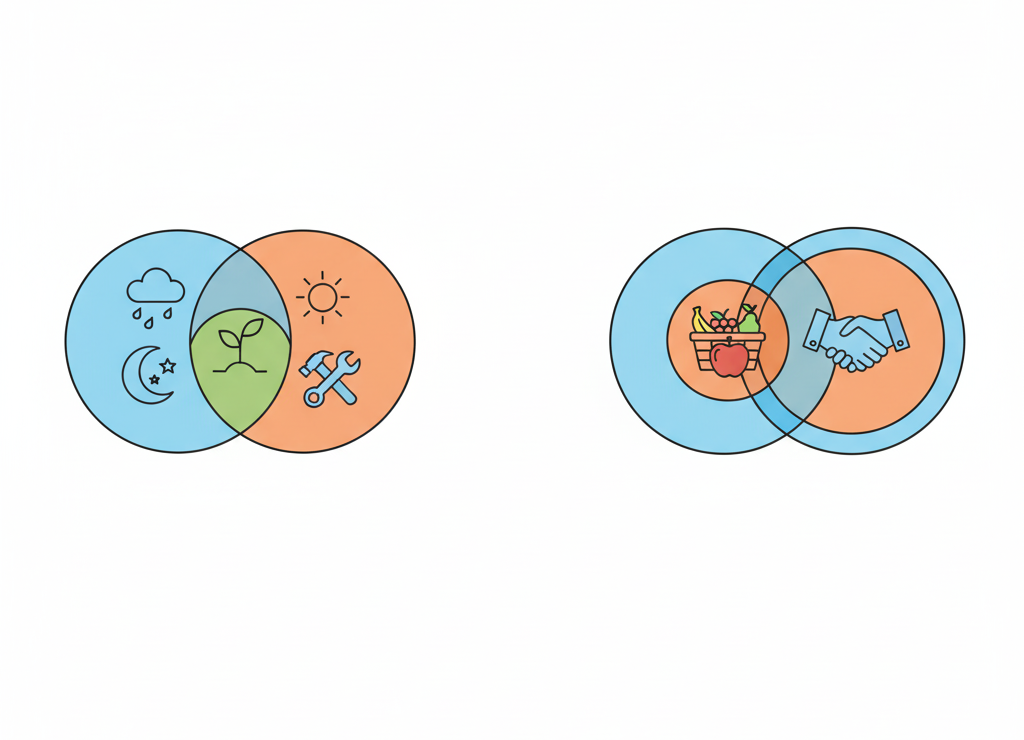
Круги Эйлера показывают, как множества связаны друг с другом
Пересекающиеся множества
Когда у двух множеств есть общие элементы, круги пересекаются.
Пример:
- Множество А — все электронные письма
- Множество В — все письма на русском языке
- Пересечение — электронные письма на русском языке
Непересекающиеся множества
Когда общих элементов нет, круги не касаются друг друга.
Пример:
- Множество А — печатные учебники
- Множество В — электронные учебники
- У них нет общих элементов (учебник не может быть одновременно печатным и электронным)
Подмножество
Когда все элементы одного множества входят в другое, маленький круг рисуется внутри большого.
Пример:
- Множество А — все ученики школы
- Множество В — шестиклассники
- Все шестиклассники — это ученики, поэтому В находится внутри А
Равные множества
Когда множества состоят из одних и тех же элементов, круги полностью совпадают.
Пример:
- Множество А — равносторонние прямоугольники
- Множество В — квадраты
- Это одно и то же! (Равносторонний прямоугольник = квадрат)
Отношение «входит в состав»
Любой сложный объект можно «разобрать» на части. Давай разберёмся, как это работает!
Компьютер — это целое или части?
Смотря для чего!
- Если считаем компьютеры в классе — это целое («в классе 15 компьютеров»)
- Если изучаем, как он работает — смотрим на части (процессор, память, жёсткий диск, монитор, клавиатура)
Из одинаковых частей
Объект может состоять из похожих элементов:
- Апельсин → дольки апельсина
- Класс → ученики
- Лес → деревья
Из разных частей
Объект может состоять из непохожих элементов:
- Компьютер → системный блок, монитор, клавиатура, мышь
- Велосипед → рама, колёса, руль, педали, цепь
- Дом → фундамент, стены, крыша
Схема состава: разбираем дом!
Давай «разберём» дом на части по порядку — от крупных деталей к мелким.
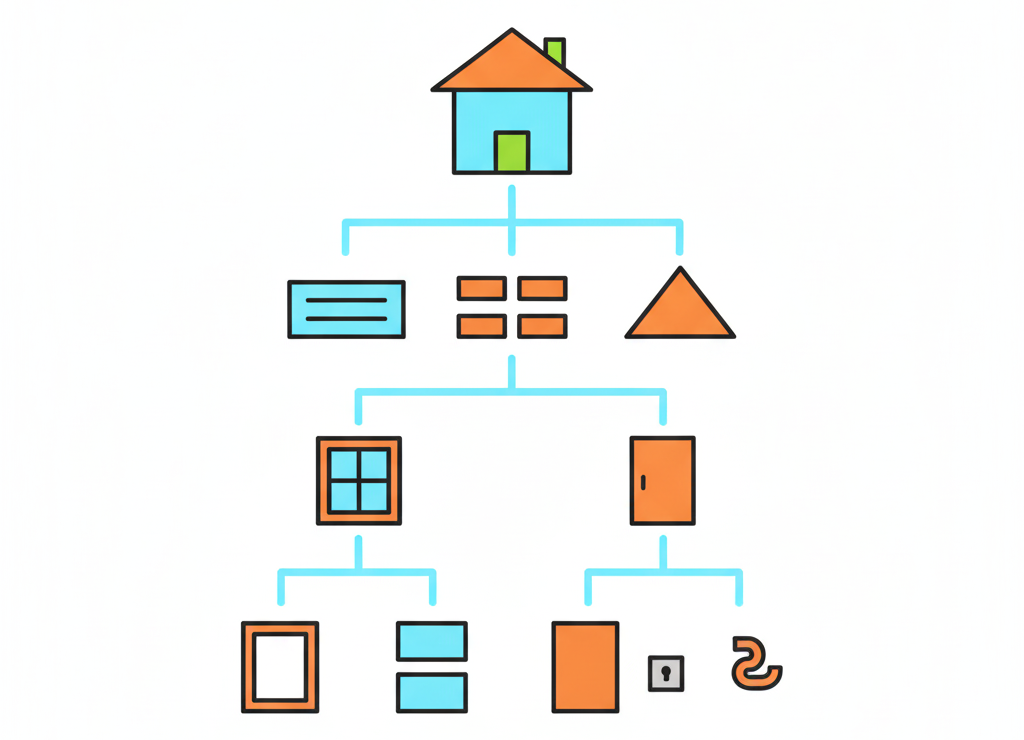
Схема состава показывает, из каких частей состоит объект
Шаг 1: Крупные части дома
- Фундамент
- Стены
- Крыша
Шаг 2: Разбираем стены подробнее
Стена состоит из:
- Окна
- Двери
Шаг 3: Разбираем окно и дверь
Окно состоит из:
- Рамы
- Стёкол
Дверь состоит из:
- Дверного полотна
- Замка
- Ручки
Важно понимать!
Всё это можно нарисовать в виде схемы состава — дерева, где вверху находится целый объект, а ниже — его части, ещё ниже — части частей.
Схема состава показывает не только части объекта, но и порядок «разборки» — то есть структуру объекта.
Общее или конкретное?
Когда мы описываем состав, мы можем говорить:
- О конкретном объекте («мой дом состоит из...»)
- Об общем представлении («дома обычно состоят из...»)
Второй вариант отвечает на вопрос: «Из чего ОБЫЧНО состоят объекты этого вида?»
Признаки составных объектов
При описании сложного объекта мы можем называть признаки как всего объекта, так и его частей!
Пример с домом
Действия с целым домом:
- Строить
- Ремонтировать
Действия с частями:
- Крышу — красить
- Стекло — вставлять
Характеристики целого дома:
- Длина
- Ширина
- Высота
Характеристики частей:
- Стены — толщина
- Крыша — высота
Самое главное
Давайте подведём итоги всего, что мы узнали об отношениях объектов:
Вопросы для самопроверки
Проверь, как хорошо ты усвоил материал!
1. Каким образом выражаются отношения между объектами? Назови имя отношения в каждом предложении.
Какое имя можно будет дать отношению, если имена объектов в предложении поменять местами? В каких парах имя отношения при этом не изменится?
- а) Колобок поёт песню Лисе.
- б) Конёк-Горбунок помогает Ивану.
- в) Пилюлькин лечит Сиропчика.
- г) Страшила путешествует вместе с Элли.
2. Придумай свои примеры для разных типов отношений
Для каждого отношения придумай 2-3 собственных примера:
| Отношение | Пример из учебника | Твой пример |
|---|---|---|
| Целое — часть | Окунь — плавник | ? |
| Вид — род | Ландыш — цветок | ? |
| Следование | Понедельник — вторник | ? |
| Причина — следствие | Жара — жажда | ? |
3. Определи отношение для каждой пары объектов
Пары объектов:
- а) пианино и музыкальный инструмент
- б) процессор и системный блок
- в) Новосибирск и город
- г) лазерный диск и информационный носитель
- д) бабочка и насекомое
- е) шестиклассник и ученик
Отношения на выбор:
- входит в состав
- является элементом множества
- является разновидностью
4. Определи множества на диаграмме (задача про европейские города)
Посмотри на рисунок из учебника (три пересекающихся круга с городами). Определи, какой круг соответствует множеству:
- а) «европейский город»
- б) «город в Англии»
- в) «столичный европейский город»
Перечисли города-объекты, являющиеся элементами представленных на рисунке множеств.
5. Задача про пересечение и объединение множеств
В одном множестве 40 элементов, а в другом — 30 элементов.
Какое максимальное количество элементов может быть в их:
- а) пересечении — множестве, которому принадлежат те и только те элементы, которые одновременно принадлежат всем исходным множествам;
- б) объединении — множестве, содержащем в себе все элементы исходных множеств?
Подсказка: Нарисуй два круга Эйлера и подумай о крайних случаях!
6. Задача про детский сад и сладости
В детском саду 52 ребёнка. Каждый из них любит конфеты или мороженое (или и то, и другое!).
- Половина детей любит конфеты
- 20 человек любят И конфеты, И мороженое
Вопросы:
- Сколько детей любит мороженое?
- Сколько детей любит ТОЛЬКО мороженое (без конфет)?
Подсказка: Нарисуй два пересекающихся круга Эйлера — это поможет!
7. Собери пары объектов с отношением «входит в состав»
Проведи мозговой штурм! Из этих слов составь шесть пар объектов, связанных отношением «входит в состав»:
Слова: колесо, дом, покрышка, окно, дверь, стекло, автомобиль
В каждой паре определи, какой объект является частью другого.
Вопрос на подумать: Какие имена объектов приведены в списке: общие или единичные?
8. Придумай действия с целым объектом и его частью
Для каждой из приведённых пар «объект — его часть» назови действие, которое можно выполнять со всем объектом, и действие, которое можно выполнять с его частью:
- а) ботинок и шнурок
- б) абрикос и косточка в нём
- в) дверь и дверной замок
Пример: Велосипед и колесо — велосипед можно катить, а колесо можно накачать.
9. Детективная задача про посылку от бабушки
Бабушка прислала Ивану посылку с яблоками и грушами.
Что известно:
- Некоторые плоды большие, остальные — маленькие
- Некоторые плоды жёлтые, остальные — зелёные
- Среди плодов не было ни маленьких груш, ни маленьких зелёных яблок
- Яблок было 25 штук
- Груш было 17 штук
- Больших плодов было 32 штуки
- Жёлтых плодов было 28 штук
- Зелёных яблок было на 2 больше, чем зелёных груш
Вопрос: Иван угостил этими плодами своих друзей. Больше всего ребятам понравились большие жёлтые яблоки. Сколько было таких яблок?
Подсказка: Начни с подсчёта общего количества плодов, потом используй информацию о размерах и цветах. Можно нарисовать таблицу или схему!
Практические задания
Попробуй применить полученные знания на практике!
Задание 1: Нарисуй схему отношений
В твоём классе есть несколько ребят, которые дружат между собой. Нарисуй схему их дружеских отношений. Используй круги для обозначения людей и линии для обозначения дружбы.
Вопрос: Нужны ли в этой схеме стрелки? Почему?
Задание 2: Создай схему состава
Выбери любой сложный объект (велосипед, смартфон, рюкзак) и создай схему его состава. Разбери объект на крупные части, затем каждую часть — на более мелкие.
Задание 3: Множества в твоей жизни
Придумай два множества из твоей жизни, которые:
- а) пересекаются
- б) не пересекаются
- в) одно является подмножеством другого
Нарисуй круги Эйлера для каждого случая.
Задание 4: Найди отношения
Выбери любые три объекта в классе и опиши все возможные отношения между ними. Используй разные типы отношений: «выше», «входит в состав», «находится рядом» и т.д.
Интересные факты
Немного познавательной информации об отношениях и множествах!
Леонард Эйлер
Леонард Эйлер (1707-1783) — великий швейцарский математик. Он придумал круги для изображения множеств, чтобы упростить решение логических задач. Эйлер был настолько продуктивным учёным, что его работы печатали ещё 50 лет после его смерти!
Множества вокруг нас
Отношения между множествами встречаются повсюду: учебные предметы в школе, жанры музыки, виды спорта, категории в интернет-магазинах. Понимание этих отношений помогает лучше организовывать информацию!
Схемы в науке
Учёные используют схемы отношений для изображения самых разных вещей: родственных связей в биологии, химических реакций, структуры организаций, связей между компьютерами в сети.
Базы данных
Когда программисты создают базы данных (например, для социальных сетей), они используют схемы отношений, чтобы показать, как связаны разные объекты: пользователи, посты, комментарии, лайки.