Схемы
Привет! Сегодня мы узнаем, как схемы помогают нам понимать сложные вещи простым способом. Научимся рисовать графы, деревья и даже решать интересные задачи. Готов к путешествию в мир схем? Тогда начинаем!

Что такое схема?
Представь, что тебе нужно объяснить другу, как добраться до твоего дома, или показать, где какие комнаты в квартире. Рисовать всё в мельчайших подробностях долго и сложно. Зато можно нарисовать схему — простой рисунок, на котором показано только самое главное!
💡 Определение
Схема — это изображение объекта, где показаны его основные черты с помощью условных обозначений.
🗺️ Схемы вокруг нас
Схемы окружают нас повсюду:
- Схема метро — показывает станции и пересадки
- План торгового центра — помогает найти нужный магазин
- Схема кинотеатра — показывает расположение мест
- Карта маршрута автобуса — какие остановки проезжает автобус
Схемы внешнего вида
Давайте посмотрим, какие бывают схемы!

Схема зрительного зала помогает выбрать удобное место
🏠 План квартиры
Такая схема показывает, где находятся комнаты, кухня, ванная. По ней можно понять размеры помещений и как они расположены. Это очень важно, когда семья выбирает новую квартиру!
🗺️ Географическая карта
Карта — это тоже схема! Она показывает города, реки, дороги. Но на карте всё уменьшено по специальному масштабу.
Туристический маршрут «Золотое кольцо России» на схеме
⚡ Важная особенность схем
Схемы показывают главное, но не всё! На схеме кинотеатра ты видишь места, но не узнаешь, какие кресла мягкие. На карте видишь города, но не узнаешь, сколько там жителей.
Схема — это информационная модель, которая выделяет один или несколько важных признаков объекта.
Графы — схемы связей
А теперь познакомимся с особым видом схем — графами!
💡 Что такое граф?
Граф — это схема, состоящая из вершин (кружочков, квадратиков, точек) и линий, которые их соединяют.
📏 Ребро
Линия без стрелки. Используется, когда связь двухсторонняя (например, друзья переписываются друг с другом).
➡️ Дуга
Линия со стрелкой. Используется, когда связь односторонняя (например, Юра пишет Ане, но Аня не отвечает).
Граф показывает, кто с кем дружит и переписывается
Типы графов
Графы бывают разными, и каждый тип подходит для своих задач.
↔️ Вершины соединены рёбрами
Пример: Схема дружбы — Юра и Аня друзья, связь двухсторонняя.
➡️ Вершины соединены дугами
Пример: Кто кому пишет письма — Юра пишет Ане (односторонняя связь).
⚖️ Есть дополнительная информация
Пример: Граф городов с расстояниями в километрах или годами основания.
📖 Важные термины
- Цепь — это путь по вершинам и рёбрам графа (например: Юра → Аня → Витя → Коля)
- Цикл — это цепь, которая возвращается в начальную точку (например: Аня → Коля → Витя → Аня)
- Петля — линия, выходящая из вершины и входящая в неё же
Взвешенные графы
Иногда на графе нужно показать дополнительную информацию — вес. Это может быть число, дата или другие данные.
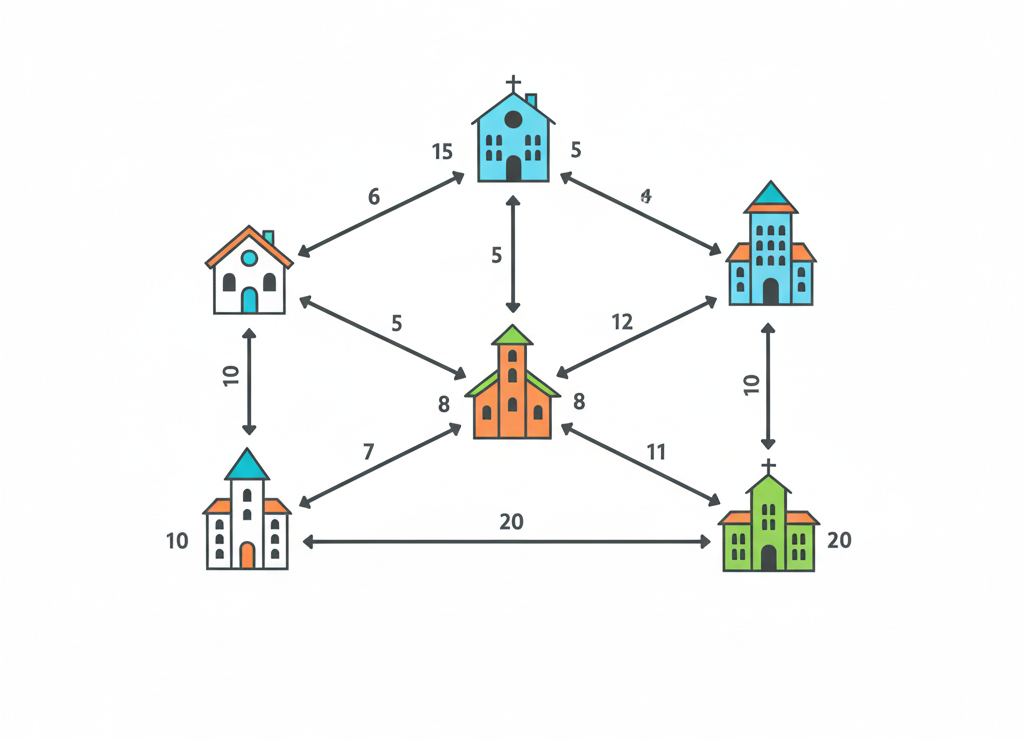
Взвешенный граф с расстояниями между городами
🌟 Пример: Граф городов Золотого кольца
- Вес вершин — годы основания городов (Москва — 1147, Владимир — 1108)
- Вес рёбер — расстояния между городами в километрах
Такой граф помогает спланировать путешествие: выбрать самый короткий маршрут или узнать, какой город древнее.
🔄 Сети
Если в графе есть циклы (можно вернуться в начальную точку разными путями), такой граф называется сетью.
Семантические сети
Это особый вид графа, где все связи разные и их нужно подписывать!
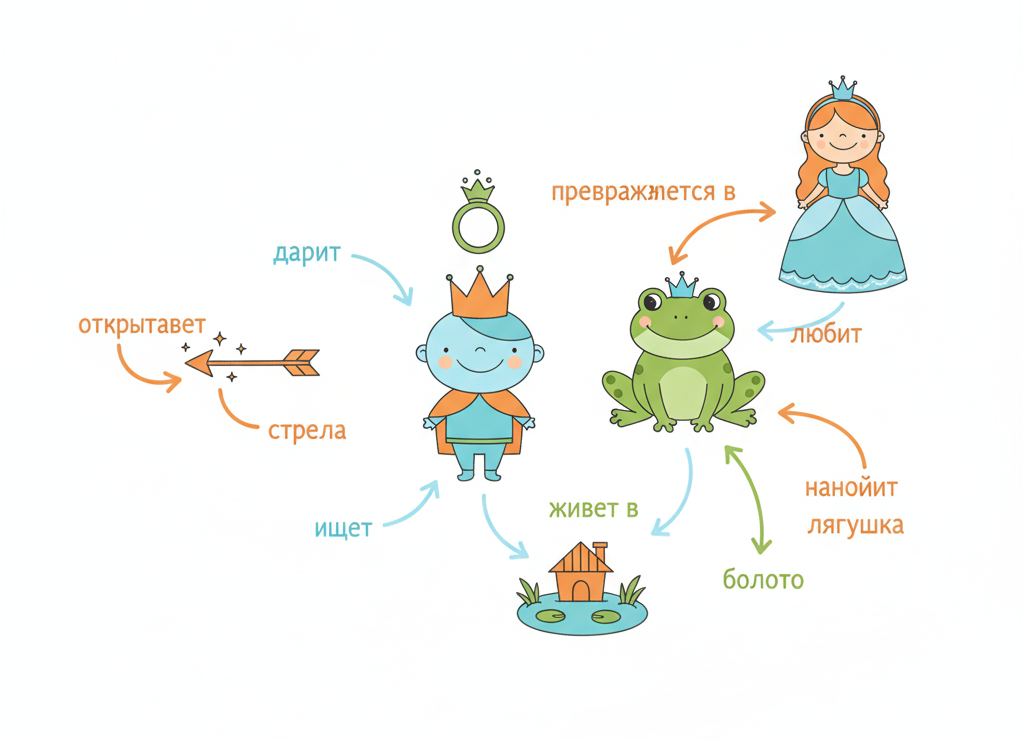
Семантическая сеть по сказке про Царевну-лягушку
📚 Пример из сказки «Царевна-лягушка»
- Иван-царевич → искал → Царевну-лягушку
- Царевна-лягушка → превратилась в → Василису Прекрасную
- Кощей → похитил → Василису Прекрасную
Семантическая сеть показывает, как связаны персонажи и предметы в сказке.
✨ Интересный факт
Считается, что любую информацию можно представить в виде семантической сети, на которой будут отражены объекты (понятия) и связи (отношения) между ними.
Деревья — особые графы
А теперь познакомимся с самым интересным типом графов — деревьями!
💡 Что такое иерархия?
Иерархия — это когда объекты расположены от главного к менее важному, от высшего к низшему.
Например, в школе:
- Директор (главный)
- Завучи (подчиняются директору)
- Учителя (подчиняются завучам)
- Ученики (подчиняются учителям)
Структура дерева: от корня к листьям
🌳 Что такое дерево?
Дерево — это граф иерархической системы.
Главные особенности дерева:
- Есть одна главная вершина — корень дерева
- Между любыми двумя вершинами только один путь
- Нет циклов и петель
- Каждая вершина (кроме корня) имеет только одного предка
- Вершины без потомков называются листьями
Примеры деревьев
Деревья встречаются во многих областях. Давайте рассмотрим несколько примеров!
💻 Прикладное ПО компьютера
Прикладное ПО
├── Текстовые редакторы
├── Графические редакторы
├── Браузеры
└── Игры
🦎 Классификация рептилий
Рептилии
├── Черепахи
├── Крокодилы
├── Клювоголовые
└── Чешуйчатые
├── Ящерицы
└── Змеи
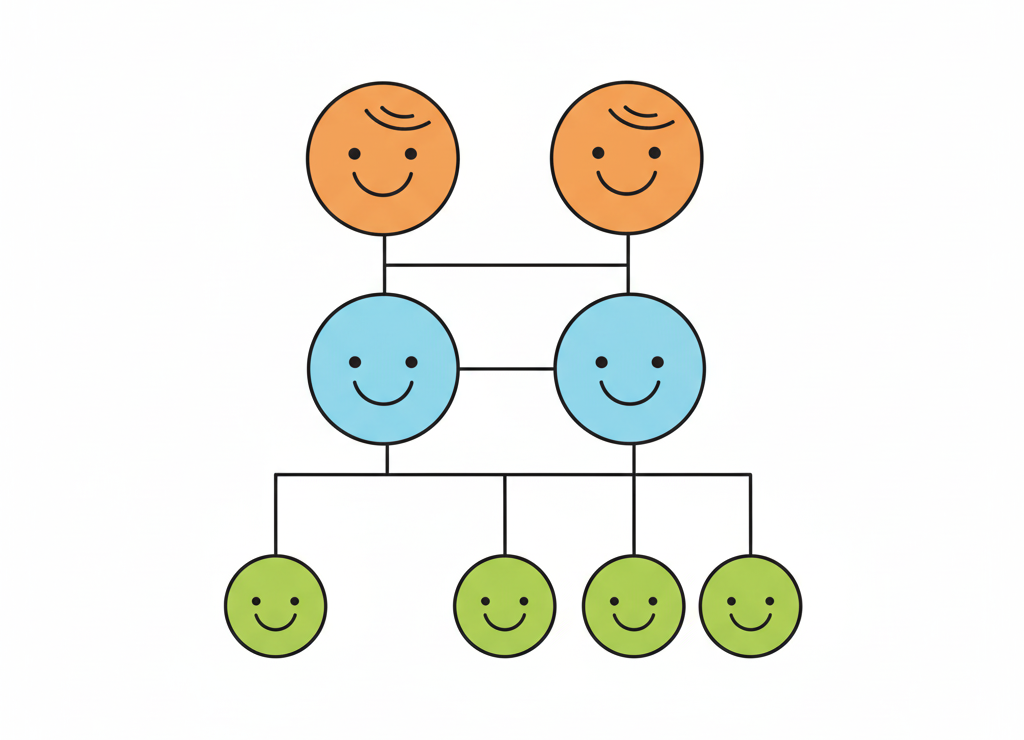
Классификация рептилий в виде дерева
📁 Файловая система
Когда ты открываешь папки на компьютере, ты видишь дерево файлов! В главной папке лежат другие папки, в них — ещё папки и файлы. Это классический пример дерева.
👨👩👧👦 Родословное дерево
Схема, показывающая родственные связи в семье. Можно рисовать от предков к потомкам или наоборот — как тебе удобнее!
Генеалогическое дерево семьи
Решаем задачи с помощью деревьев
Деревья очень помогают решать задачи на перебор вариантов! Давайте попробуем!
📝 Задача 1: Рассаживаем учеников
Условие: Нужно посадить трёх учеников (Аня, Боря, Вася) на три стула в ряд. Сколькими способами это можно сделать?
Решение:
- Первый стул: можем посадить любого из трёх — А, Б или В (3 варианта)
- Второй стул: остались 2 человека (2 варианта для каждого случая)
- Третий стул: остался 1 человек (1 вариант)
Рисуем дерево:
- От корня идут 3 ветви (А, Б, В)
- От каждой из них — 2 ветви (оставшиеся люди)
- От каждой из них — 1 ветвь (последний человек)

Дерево вариантов рассаживания учеников
✅ Все варианты:
- А–Б–В
- А–В–Б
- Б–А–В
- Б–В–А
- В–А–Б
- В–Б–А
Ответ: 6 способов
Быстрый способ без дерева: 3 × 2 × 1 = 6
🗺️ Задача 2: Помогаем Ивану-царевичу
Условие: Иван-царевич идёт к волшебному саду. На каждой развилке — три тропинки: левая (Л), средняя (С), правая (П). Нужно пройти три развилки.
Советы ворона:
- Иди сейчас по правой тропинке (П)
- На второй развилке не выбирай правую (не П)
- На третьей развилке не ходи по левой (не Л)
Подсказка голубя: Только один совет верный! И нужно идти по тропинкам разных направлений.
Решение: Рисуем граф всех возможных маршрутов. Отмечаем цветом советы ворона. Ищем маршрут с одним цветным ребром и разными тропинками.
✅ Правильный маршрут: Средняя → Левая → Правая (С–Л–П)
📌 САМОЕ ГЛАВНОЕ
Давайте повторим ключевые понятия, которые мы изучили!
🤔 Вопросы для самопроверки
Проверь, как хорошо ты усвоил материал!
1. Вспомни схемы из жизни: Назови 2–3 схемы, которые ты видел в жизни. Что они показывают?
Подумай о:
- Схема метро
- План эвакуации в школе
- Карта торгового центра
- Схема проезда автобусов
2. Изучи план эвакуации: На каждом этаже твоей школы есть план эвакуации при пожаре. Найди его и посмотри внимательно. Какие объекты на нём нарисованы?
Подсказка: Классы, коридоры, лестницы, выходы, огнетушители...
3. Где нужны карты? В каких профессиях и занятиях людям обязательно нужны карты?
Подумай о:
- Водители и таксисты
- Туристы и путешественники
- Моряки и капитаны кораблей
- Лётчики
- Военные
- Геологи и географы
4. Угадай сказку: Представь граф, где Колобок связан с Лисой, Волком, Медведем и Зайцем. Что это за сказка?
Попробуй нарисовать такой граф и подписать связи!
5. Задача про холм: На холм ведут три тропинки. Сколькими способами можно подняться на холм и спуститься с него?
Вариант 1: Можно подниматься и спускаться по любой тропинке
Вариант 2: Нужно подниматься и спускаться по разным тропинкам
Попробуй нарисовать дерево решений!
6. Числовая задача: Сколько трёхзначных чисел можно составить из цифр 1, 3, 5, 7, если цифры не должны повторяться?
Подсказка: Используй дерево или умножение! Для первой цифры — 4 варианта, для второй — 3 варианта, для третьей — 2 варианта.
7. Подумай и обсуди: Где тебе могут пригодиться знания о схемах и графах? На каких уроках? В жизни?
Например:
- География — работа с картами
- Информатика — файловые системы
- Планирование маршрута путешествия
- Игры с квестами
- Решение головоломок
- Создание родословного дерева семьи
8. Объясни термины: Что такое вершина, ребро, дуга, цепь, цикл?
Попробуй объяснить своими словами и привести примеры.
9. Чем отличается неориентированный граф от ориентированного?
Подсказка: Подумай о направлении связей — стрелки есть или нет?
10. Что такое взвешенный граф? Приведи пример из жизни.
Вспомни про граф городов с расстояниями или годами основания.
11. Назови главные особенности дерева. Чем дерево отличается от обычного графа?
Вспомни:
- Есть ли циклы?
- Сколько путей между вершинами?
- Есть ли главная вершина?
12. Приведи 3 примера иерархических систем из жизни.
Подумай про школу, армию, компанию, государство, систему папок на компьютере...
13. Как можно представить дерево в виде текста?
Подсказка: Многоуровневый список с отступами!
🎯 Практические задания
Попробуй применить полученные знания на практике!
🎨 Задание 1: Нарисуй граф друзей
Нарисуй граф, показывающий, кто с кем дружит в твоём классе (возьми 5-6 одноклассников). Используй:
- Кружочки для ребят
- Линии для связей дружбы
Это будет неориентированный граф!
🌳 Задание 2: Создай родословное дерево
Нарисуй дерево своей семьи минимум на 3 поколения:
- Бабушки и дедушки
- Родители
- Ты и братья/сёстры
📁 Задание 3: Файловая система
Нарисуй дерево папок на своём компьютере или телефоне. Начни с главной папки и покажи, какие папки в ней лежат.
🔢 Задание 4: Числовая задача
Сколько двузначных чисел можно составить из цифр 2, 4, 6, 8, если:
- а) цифры могут повторяться?
- б) цифры не должны повторяться?
Попробуй решить с помощью дерева!
🎭 Задание 5: Семантическая сеть
Выбери любимую сказку или мультфильм. Нарисуй семантическую сеть с персонажами и подпиши связи между ними (кто кого любит, кто с кем дружит, кто кого спасает).
🗺️ Задание 6: Маршрут в школу
Нарисуй схему маршрута от твоего дома до школы. Отметь важные ориентиры: магазины, остановки, перекрёстки.